Question

A bullet of mass $25g$ was moving at a rate of $500m{{s}^{-1}}$. After passing through a solid substance, it continued to move at a rate of $100m{{s}^{-1}}$. How much is the work done when the bullet had to do in passing through the substance?
$\begin{align}
  & A.2000J \\
 & B.1000J \\
 & C.4000J \\
 & D.3000J \\
\end{align}$

Answer 1

Hint: Work-energy theorem states that the variation in kinetic energy of a body is equivalent to the work done by net force acting on it. The kinetic energy of an object is the energy that is possessed due to its motion. It is described as the work required to accelerate a body of a certain mass from rest to the particular velocity. Having gained this energy when it’s accelerating, the body will maintain this kinetic energy until its speed varies.

Complete step by step solution:

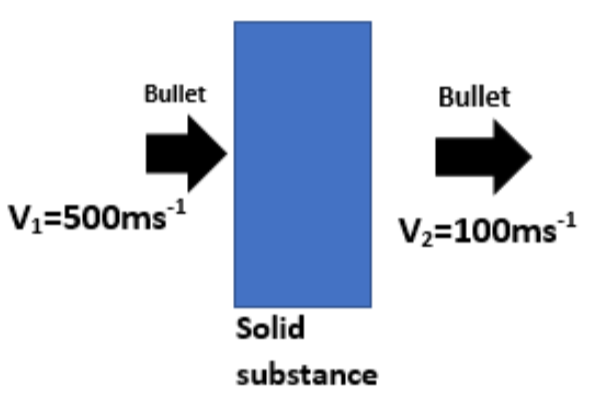
From the question, we will get to know that,
Mass of the bullet is given as,
${{m}_{1}}=25g$
Velocity at which bullet is moving,
${{v}_{1}}=500m{{s}^{-1}}$
Mass of the solid substance through which bullet is passing is ${{m}_{2}}$,
And the velocity of the bullet after passing through the solid substance,
${{v}_{2}}=100m{{s}^{-1}}$
According to the question we can say that the velocity change happened is due to the energy loss in the solid substance, so we can say that,
The velocity change
${{v}^{2}}={{v}_{1}}^{2}-{{v}_{2}}^{2}$
Substituting the value in it,
$\begin{align}
  & {{v}^{2}}={{500}^{2}}-{{100}^{2}} \\
 & =240000m{{s}^{-1}} \\
\end{align}$
$\begin{align}
  & E=\dfrac{1}{2}{{m}_{1}}{{v}^{2}} \\
 & =\dfrac{1}{2}\times 25\times {{10}^{-3}}\times {{\left( 240000 \right)}^{2}} \\
 & =3000J \\
\end{align}$
Therefore now we can calculate the energy lost in the collision,
$E=\dfrac{1}{2}{{m}_{1}}{{v}^{2}}$
Substituting the value in this equation will give,
$\begin{align}
  & E=\dfrac{1}{2}{{m}_{1}}{{v}^{2}} \\
 & =\dfrac{1}{2}\times 25\times {{10}^{-3}}\times {{\left( 240000 \right)}^{2}} \\
 & =3000J \\
\end{align}$
Hence the correct answer for the question is option D.

Note: There are three different types of collisions, elastic, inelastic, and completely inelastic. In all the cases, momentum is being conserved in all three types of collisions. What compares the collisions is that what happens to the kinetic energy. Inelastic collisions happen when the colliding objects bounce off of each other. This typically happens when we are having colliding objects which are very hard or bouncy. Inelastic collisions happen when the two objects collide and kinetic energy is not being conserved.