Question

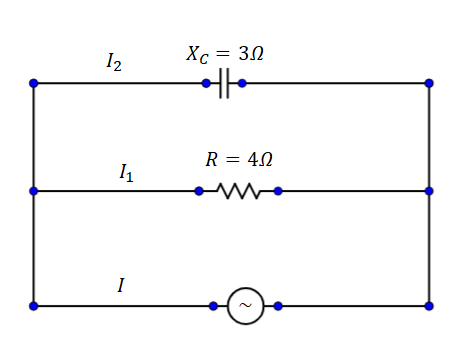
A capacitor and resistor are connected with an AC source as shown in figure. The capacitor is ${X_C} = 3\Omega $ and resistance of the resistor is$4\Omega $. Phase difference between current $I$ and${I_1}$ is \[\left[ {{{\tan }^{ - 1}}\left( {\dfrac{3}{4}} \right) = 37^\circ } \right]\] :

A. $90^\circ $
B. Zero
C. $53^\circ $
D. $37^\circ $

Answer 1

Hint:-The resultant of the capacitor resistance and the resistance of the resistor will give us the total resistance of the circuit. The current in the capacitor and in the resistor will be different as the resistance of the two elements are also different.
Formula used: The formula of the ohm's law is given by, $V = I \cdot R$ where V is the potential difference. I is the current in the circuit and R is the resistance in the circuit.

Complete step-by-step solution
Since the ohm's law is given by$V = I \cdot R$.
Where V is the potential difference. I is the current in the circuit and R is the resistance in the circuit.
The current passing through the capacitor can be calculated by,
$ \Rightarrow V = {I_2} \cdot \left( {{X_c}} \right)$
Here ${X_c}$ is the reactance of the capacitor and $V$ is${V_{rms}}$.
$ \Rightarrow {I_2} = \dfrac{V}{{{X_c}}}$
Replace the value of reactance of the capacitor, ${X_C} = 3\Omega $.
$ \Rightarrow {I_2} = \dfrac{V}{3}$.
The current of the capacitor is equal to ${I_2} = \dfrac{V}{3}$.
The current flowing in the resistor of resistance of $4\Omega $ is equal to,
$ \Rightarrow I = \dfrac{V}{R}$
$ \Rightarrow I = \dfrac{V}{4}$
The current flowing through the resistor of resistance $4\Omega $ is equal to $I = \dfrac{V}{4}$.
The current ${I_2}$ is $90^\circ $ ahead of the applied voltage and the current $I$ is in the same phase therefore the phase difference between $I$ and${I_2}$.is given by,
$ \Rightarrow \tan \phi = \dfrac{{{I_2}}}{I}$
$ \Rightarrow \tan \phi = \dfrac{{\left( {\dfrac{V}{3}} \right)}}{{\left( {\dfrac{V}{4}} \right)}}$
$ \Rightarrow \tan \phi = \dfrac{4}{3}$.
$ \Rightarrow \phi = {\tan ^{ - 1}}\left( {\dfrac{4}{3}} \right)$
$ \Rightarrow \phi = 53^\circ $.
The phase difference between current $I$ and${I_2}$.is equal to$\phi = 53^\circ $. The correct answer for this problem is option C.

Note:- The resistance offered by the capacitor in the dc circuit is infinite because the resistance offered by the capacitor is inversely proportional to the angular frequency of the circuit and the angular frequency in the dc circuit is zero.