Question

A charged particle enters a magnetic field at right angles to the field. The field exists for a length equal to $1.5$ times the radius of the circular path of the particle. The particle deviated from its path by:
A. ${90^ \circ }$
B. ${\sin ^{ - 1}}\left( {\dfrac{2}{3}} \right)$
C. $${30^ \circ }$$
D. $${180^ \circ }$$

Answer 1

Hint: We are given that the particle enters the magnetic field at right angle. The particle traces a circular path. The length of the field exceeds the radius of the circular path of the particle. We need to find the deviation of the particle from the circular path. If the length of the magnetic field is more than the radius of the circular path then the particle exits the magnetic field from the same side as it enters.

Complete step by step answer:
The force $$F$$ acting on the particle having some charge $$q$$ is given as:
$$F = q(v \times B)$$
The direction of the force is given by the cross product between the velocity and the magnetic field.
Let us draw an appropriate diagram for the same.

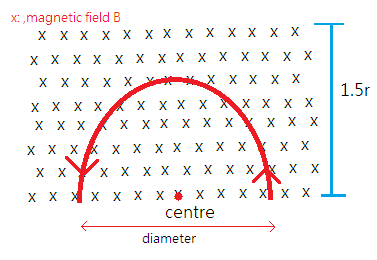
It is clear from the particle enter from the right-hand side and exits from the left-hand side. The length of the magnetic field is $$1.5r$$ where $$r$$ is the radius of the circular path that the particle is tracing. The diameter of the circular path is $$2r$$ .
For a length greater than the radius of the circular path traced by the particle, the particle exits from the same side from which it enters. Hence, the angle of deviation for the particle is $${180^ \circ }$$ .
So, the correct answer is “Option D”.

Note:
For the particle to reach the maximum displacement the field must have a minimum length which is equal to the radius of the circular path traced by the particle.
The direction force acting on the particle is perpendicular to the direction of the magnetic field is given by the cross product between velocity and magnetic field.