Question

A chess board contains $64$ equal squares and the area of each square is $6.25c{m^2}$, the border around the square is $2cm$ wide. The length of the chess board is
$
  A)\,8cm \\
  B)\,24cm \\
  C)\,12cm \\
  D)\,16cm \\
$

Answer 1

Hint:Since the chess board is a square and it actually consists of $64$ equals square boxes. The side length of each square box can be calculated since its area is given. Also there is a $2cm$ wide border on all the sides of the chess board. So, to calculate the complete length of the board, the length of borders will also be included.

Complete step-by-step answer:
The chess board contains $64$ equal squares. We know that the overall shape of the chess board is also a square.
Therefore, the chess board has $8 \times 8$ small squares.
It is mentioned in the question that the area of each small square is $6.25c{m^2}$.
We know that the area of a square is equal to the square of its side length
${\left( {side} \right)^2} = area$
$side\,length = \sqrt {area} $
$\therefore $ The side length of each of the small squares is equal to the square root of its area
$side = \sqrt {6.25} $
$side = 2.5cm$ $ \to \left( 1 \right)$
Now, it is also given that the chess board has a border in width $2cm$

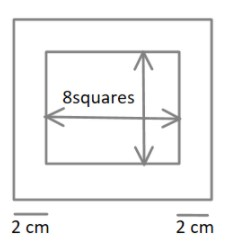
Therefore, the side length of the whole chess board will be equal to the sum of length of small squares on one side and the width of the border on the two sides.
$Total\,length = 8 \times length\,of\,one\,small\,square + 2 \times width\,of\,the\,\,border$
$Total\,length = 8 \times 2.5 + 2 \times 2$
$Total\,length = 20 + 4 = 24cm$

So, the correct answer is “Option B”.

Note:It should be noted that borders will exist on the both sides when the total length of the chess board is to be considered.Each statement given in the question needs to be understood carefully while converting them in mathematical form.