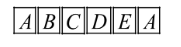Answer
500.1k+ views
Hint: Use basic definition of probability:
$P\left( E \right)=\dfrac{\text{Total number favourable to cases}}{\text{Total outcomes (sample space)}}$
As we know that $P\left( E \right)=\dfrac{\text{ Number of outcomes required}}{\text{sample space (Total no}\text{. of outcomes)}}$
Here, As we can observe that we have six faces on a die with six letters, i.e., the number of total outcomes will be 6.
Let categorise the number of times letters can come by counting the number of faces at which they are present:
$\begin{align}
& A=2 \\
& B=1 \\
& C=1 \\
& D=1 \\
& E=1 \\
\end{align}$
Hence, for any face’s letter probability
$P\left( E \right)=\dfrac{\text{Outcome of that particular letter}}{\text{Total number of outcomes }}$
(i) Probability for getting $A$
\[\begin{align}
& P\left( E \right)=\dfrac{\text{No}\text{. of times A can come to a face}}{\text{Total number of outcomes possible }} \\
& P\left( E \right)=\dfrac{2}{6}=\dfrac{1}{3} \\
\end{align}\]
(ii) Probability for getting $D$
\[\begin{align}
& P\left( E \right)=\dfrac{\text{No}\text{. of times D can come to a face}}{\text{Total number of outcomes possible }} \\
& P\left( E \right)=\dfrac{1}{6} \\
\end{align}\]
Note: (i) One can take the total number of outcomes as $5$ as counting the number of letters present $A,B,C,D,E$ which will be wrong because we are calculating probability with respect to the faces (once thrown written in the question).
(ii) One can think, this problem belongs to any application part of probability but here it is using the fundamental definition.
$P\left( E \right)=\dfrac{\text{Total number favourable to cases}}{\text{Total outcomes (sample space)}}$
As we know that $P\left( E \right)=\dfrac{\text{ Number of outcomes required}}{\text{sample space (Total no}\text{. of outcomes)}}$
Here, As we can observe that we have six faces on a die with six letters, i.e., the number of total outcomes will be 6.
Let categorise the number of times letters can come by counting the number of faces at which they are present:
$\begin{align}
& A=2 \\
& B=1 \\
& C=1 \\
& D=1 \\
& E=1 \\
\end{align}$
Hence, for any face’s letter probability
$P\left( E \right)=\dfrac{\text{Outcome of that particular letter}}{\text{Total number of outcomes }}$
(i) Probability for getting $A$
\[\begin{align}
& P\left( E \right)=\dfrac{\text{No}\text{. of times A can come to a face}}{\text{Total number of outcomes possible }} \\
& P\left( E \right)=\dfrac{2}{6}=\dfrac{1}{3} \\
\end{align}\]
(ii) Probability for getting $D$
\[\begin{align}
& P\left( E \right)=\dfrac{\text{No}\text{. of times D can come to a face}}{\text{Total number of outcomes possible }} \\
& P\left( E \right)=\dfrac{1}{6} \\
\end{align}\]
Note: (i) One can take the total number of outcomes as $5$ as counting the number of letters present $A,B,C,D,E$ which will be wrong because we are calculating probability with respect to the faces (once thrown written in the question).
(ii) One can think, this problem belongs to any application part of probability but here it is using the fundamental definition.
Recently Updated Pages
Fill in the blanks with suitable prepositions Break class 10 english CBSE

Fill in the blanks with suitable articles Tribune is class 10 english CBSE

Rearrange the following words and phrases to form a class 10 english CBSE

Select the opposite of the given word Permit aGive class 10 english CBSE

Fill in the blank with the most appropriate option class 10 english CBSE

Some places have oneline notices Which option is a class 10 english CBSE

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

How do you graph the function fx 4x class 9 maths CBSE

When was Karauli Praja Mandal established 11934 21936 class 10 social science CBSE

Which are the Top 10 Largest Countries of the World?

What is the definite integral of zero a constant b class 12 maths CBSE

Why is steel more elastic than rubber class 11 physics CBSE

Distinguish between the following Ferrous and nonferrous class 9 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE