Question

A child makes a poster on a chart paper drawing a square ABCD of side 14 cm She A child makes a poster on a chart paper drawing a set inside with centre A B C and D in which she suggests different ways to save energy. The circles are drawn in such a way that each circle touches off the three remaining circles (In the shaded region she writes a message Save Energy. Find the perimeter and area of the shaded region.

Answer 1

Hint: Type of questions are based on the perimeter area calculation. But these rather than simple calculations of perimeter or area give us some complex shape and ask us to find out the perimeter or area of the complex shape. Then for this we had to find out the element of complex shape of which we can know the dimensions or which we know.

Complete step by step answer:
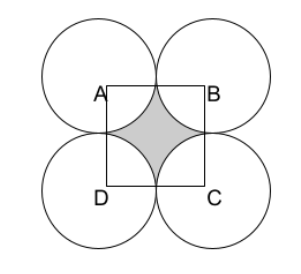
As in our case we have a circle, through which we got some shape highlighted through shade, enclosed in a square ABCD with an unit length of \[14cm\] , where $ A,B,C,D $ are the centre of the circle (as given in the question). We can easily say that line $ \overrightarrow{AB} $ and line $ \overrightarrow{AD} $ are perpendicular to each other, as they are adjacent sides of square, so we can say that the quarter part of square forms the quadrant for the circle. Hence the arc will have an angle of $ 90{}^\circ $ . Hence we say that the complex shape represented in the shaded region is formed by the combination of arcs of 4 circles, of which all 4 arcs must be of equal length as there is symmetry.
So, solving the question, first we will find the length of arc of any one circle which also helps in making the shaded region then we will multiply by 4 to find the perimeter of the shaded region, as shaded region is made by combining 4 such arc of circle and these arc will be equal as whole figure have symmetry.
As we know that length of arc is $ =\dfrac{\theta }{360{}^\circ }2\pi r $ , $ \theta $ is the angle formed by arc at the centre, ‘r’ is the radius of circle which is \[7\text{ }cm\] . In \[{{1}^{st}}\] circle i.e. circle with centre ‘A’ arc length that have part in forming the shaded region will be;
 $ \begin{align}
  & =\dfrac{\theta }{360{}^\circ }2\pi r \\
 & =\dfrac{90{}^\circ }{360{}^\circ }2\pi \times 7 \\
 & =\dfrac{1}{4}\times 2\pi \times 7 \\
 & =\dfrac{1}{4}\times 2\times \dfrac{22}{7}\times 7 \\
 & =11 \\
\end{align} $
So arc length is $ 11cm $ .
Total perimeter of shaded region will be equal to arc length multiplied by 4. So total perimeter of shaded region
  $ \begin{align}
  & =11\times 4 \\
 & =44cm \\
\end{align} $
Hence the perimeter of the shaded region is \[44\text{ }cm\] .
Similarly for the area of the shaded region, we can find the area of square whose length is 14 cm as given in the question subtracting it with the area of the quadrant of circles, which will give the area of the shaded region. So area of square will be equal to \[length\times length\] i.e. $ {{l}^{2}} $ ; so area will be;
 $ {{\left( 14 \right)}^{2}}=196 $
As we know that area of quadrant of a circle is \[=\dfrac{\theta }{360{}^\circ }\pi {{r}^{2}}\] in which r is the radius and $ \theta $ is the angle that will form the quadrant. So area of quadrant will be;
 \[\begin{align}
  & =\dfrac{\theta }{360{}^\circ }\pi {{r}^{2}} \\
 & =\dfrac{{{90}^{\circ }}}{360{}^\circ }\pi {{\left( 7 \right)}^{2}} \\
 & =\dfrac{1}{4}\times \dfrac{22}{7}\times \left( 49 \right) \\
 & =\dfrac{77}{2} \\
\end{align}\]
So multiply it by four as there are total four such circles which are taking part to form a shaded region, so we will have area of all four quadrant of circle equal to
 $ \begin{align}
  & =\dfrac{77}{2}\times 4 \\
 & =154 \\
\end{align} $
Now subtract it from the area of circle to find out the area of shaded region, so we will get;
 $ 196-154=42 $
Hence the area of shaded region is $ 42c{{m}^{2}} $

Note: For the type of question always aim to figure out the simple shape whose area or perimeter you can find out easily, as in our case we find out the arc, whose length we can calculate easily if we know the angle formed by arc at centre, which is $ 90{}^\circ $ in our case, as according to question square is formed.