Question

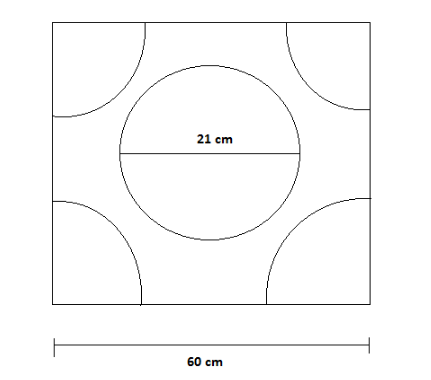
A child prepares a poster on ‘Save energy’ on a square sheet whose each side measures 60 cm. At each corner of the sheet, she draws a quadrant of radius 17.5 cm in which she shows the ways to save energy. At the center, she draws a circle of diameter 21 cm and writes slogan in it. Write down the number of ways equal to the number of quadrants by which energy can be saved.

Answer 1

Hint: The basic thing here is to identify how many quadrants are given in the figure and write that many ways to conserve energy, for that lets recall what quadrant actually means.
Energy conservation is the effort we make to reduce the consumption of energy by using them in a proper way and without wasting them. Energy conservation is a very important process because using non-renewable resources like fossil fuels are present in our environment in limiting quantities and using them in bulk may limit their quantity for the future generations so we need to conserve them for the future generations.

Complete step-by-step answer:
The following are the definitions of the quadrant:
1.One-fourth of a circle is called a quadrant. Therefore in the above figure we are given four quadrants at four corners of the quadrilateral, hence we are supposed to give four ways of saving energy as it should be equal to the number of quadrants given in the figure.
The four ways (equal to number of quadrants given in the figure) are:
I.Switching off the fans when no one is in the room as this will help in conserving the electricity which us the source of energy.
II.Turning off the vehicles at the traffic signal, when we are stopping at a red signal we must turn off the vehicle because this will help in reducing the consumption of petrol and diesel.
III.Unplug electrical appliances when not in use because 75% of the energy is saved when we turn of the electrical appliances
IV.Using a natural source of light that is SUN in day time by removing curtains at the time of the day.


Note: A quadrant is one of four equal parts into which a circle or other shape has been divided. Therefore one can note that adding all four quadrants will give us a complete circle.
 Students must note the conservation of energy is very important because cutting back of energy results in higher quality of life, it reduces the emission of harmful gases so we get cleaner air quality and this creates a healthier planet.