
Answer
499.2k+ views
Hint: Analyze the situation with a diagram. Calculate the area of the minor sector of the circle first and then subtract the area of the triangle formed by the chord joining with the center from it.
According to the information given in the question, consider the above figure. We have to calculate the area of the minor segment of the circle divided by chord AB. Clearly, the minor segment of the circle is lying at the bottom of chord AB.
AB is subtending angle ${60^ \circ }$ at the center and the radius of the circle is 14 cm.
Area of circle $ = \pi \times {\left( {14} \right)^2} = 196\pi $
Area of sector OAB of circle $ = \dfrac{{{{60}^ \circ }}}{{{{360}^ \circ }}} \times 196\pi = \dfrac{1}{6} \times 196\pi $
Now, $\Delta OAB$ is an isosceles triangle because OA and OB are the radius of the circle. We know that:
Area of triangle $ = \dfrac{1}{2}ab\sin \theta $, applying this formula $\Delta OAB$, we’ll get:
$ \Rightarrow $Area ($\Delta OAB$) $ = \dfrac{1}{2} \times OA \times OB \times \sin {60^ \circ } = \dfrac{1}{2} \times 14 \times 14 \times \dfrac{{\sqrt 3 }}{2}$,
$ \Rightarrow $Area ($\Delta OAB$) $ = 49\sqrt 3 $
Now the area of minor segment is equal to the difference between the area of sector OAB and area of triangle AOB:
$ \Rightarrow $Area of minor segment $ = \dfrac{1}{6} \times 196\pi - 49\sqrt 3 = \dfrac{{196 \times 22}}{{6 \times 7}} - 84.87$,
$ \Rightarrow $Area of minor segment $ = 102.67 - 84.87 = 17.8$
Thus the area of the minor segment is 17.8 square cm.
Note: If $\theta $is the angle subtended by a sector of a circle of radius r at the center, then the area of the sector is given as:
$ \Rightarrow $Area of sector $ = \dfrac{\theta }{{{{360}^ \circ }}} \times \pi {r^2}$
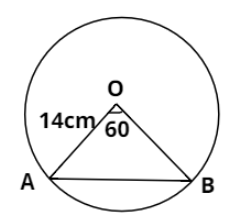
According to the information given in the question, consider the above figure. We have to calculate the area of the minor segment of the circle divided by chord AB. Clearly, the minor segment of the circle is lying at the bottom of chord AB.
AB is subtending angle ${60^ \circ }$ at the center and the radius of the circle is 14 cm.
Area of circle $ = \pi \times {\left( {14} \right)^2} = 196\pi $
Area of sector OAB of circle $ = \dfrac{{{{60}^ \circ }}}{{{{360}^ \circ }}} \times 196\pi = \dfrac{1}{6} \times 196\pi $
Now, $\Delta OAB$ is an isosceles triangle because OA and OB are the radius of the circle. We know that:
Area of triangle $ = \dfrac{1}{2}ab\sin \theta $, applying this formula $\Delta OAB$, we’ll get:
$ \Rightarrow $Area ($\Delta OAB$) $ = \dfrac{1}{2} \times OA \times OB \times \sin {60^ \circ } = \dfrac{1}{2} \times 14 \times 14 \times \dfrac{{\sqrt 3 }}{2}$,
$ \Rightarrow $Area ($\Delta OAB$) $ = 49\sqrt 3 $
Now the area of minor segment is equal to the difference between the area of sector OAB and area of triangle AOB:
$ \Rightarrow $Area of minor segment $ = \dfrac{1}{6} \times 196\pi - 49\sqrt 3 = \dfrac{{196 \times 22}}{{6 \times 7}} - 84.87$,
$ \Rightarrow $Area of minor segment $ = 102.67 - 84.87 = 17.8$
Thus the area of the minor segment is 17.8 square cm.
Note: If $\theta $is the angle subtended by a sector of a circle of radius r at the center, then the area of the sector is given as:
$ \Rightarrow $Area of sector $ = \dfrac{\theta }{{{{360}^ \circ }}} \times \pi {r^2}$

Recently Updated Pages
Fill in the blanks with suitable prepositions Break class 10 english CBSE

Fill in the blanks with suitable articles Tribune is class 10 english CBSE

Rearrange the following words and phrases to form a class 10 english CBSE

Select the opposite of the given word Permit aGive class 10 english CBSE

Fill in the blank with the most appropriate option class 10 english CBSE

Some places have oneline notices Which option is a class 10 english CBSE

Trending doubts
How do you graph the function fx 4x class 9 maths CBSE

When was Karauli Praja Mandal established 11934 21936 class 10 social science CBSE

What is the definite integral of zero a constant b class 12 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Change the following sentences into negative and interrogative class 10 english CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

Explain the Treaty of Vienna of 1815 class 10 social science CBSE

Discuss the main reasons for poverty in India

Write a letter to the principal requesting him to grant class 10 english CBSE




