Question

A circle and a parabola intersect in four points; show that the algebraic sum of the ordinates of the four points is zero.
Also show that the line joining one pair of these four points and the line joining the other pair are equally inclined to the axis.

Answer 1

Hint: Assume any four points of the form $\left( a{{t}^{2}},2at \right)$ parabola intersect. Prove that the sum of their ordinate, ${{t}_{1}}+{{t}_{2}}+{{t}_{3}}+{{t}_{4}}=0$. Then use the slope formula to find slope of $1\ and\ 2$, and point $3\ and\ 4$. Equate them and prove they are equally inclined to the axis.

Complete step-by-step solution -
Let us consider that the circle is of the form,
${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0............\left( 1 \right)$
Let the parabola be of the form $:{{y}^{2}}=4ax..........\left( 2 \right)$
It’s told that the circle and parabola intersect at $4$ points.
Let us take any point on the parabola, which is of the form$\left( a{{t}^{2}},2at \right)$
i.e., $x=a{{t}^{2}},y=2at..........\left( 3 \right)$

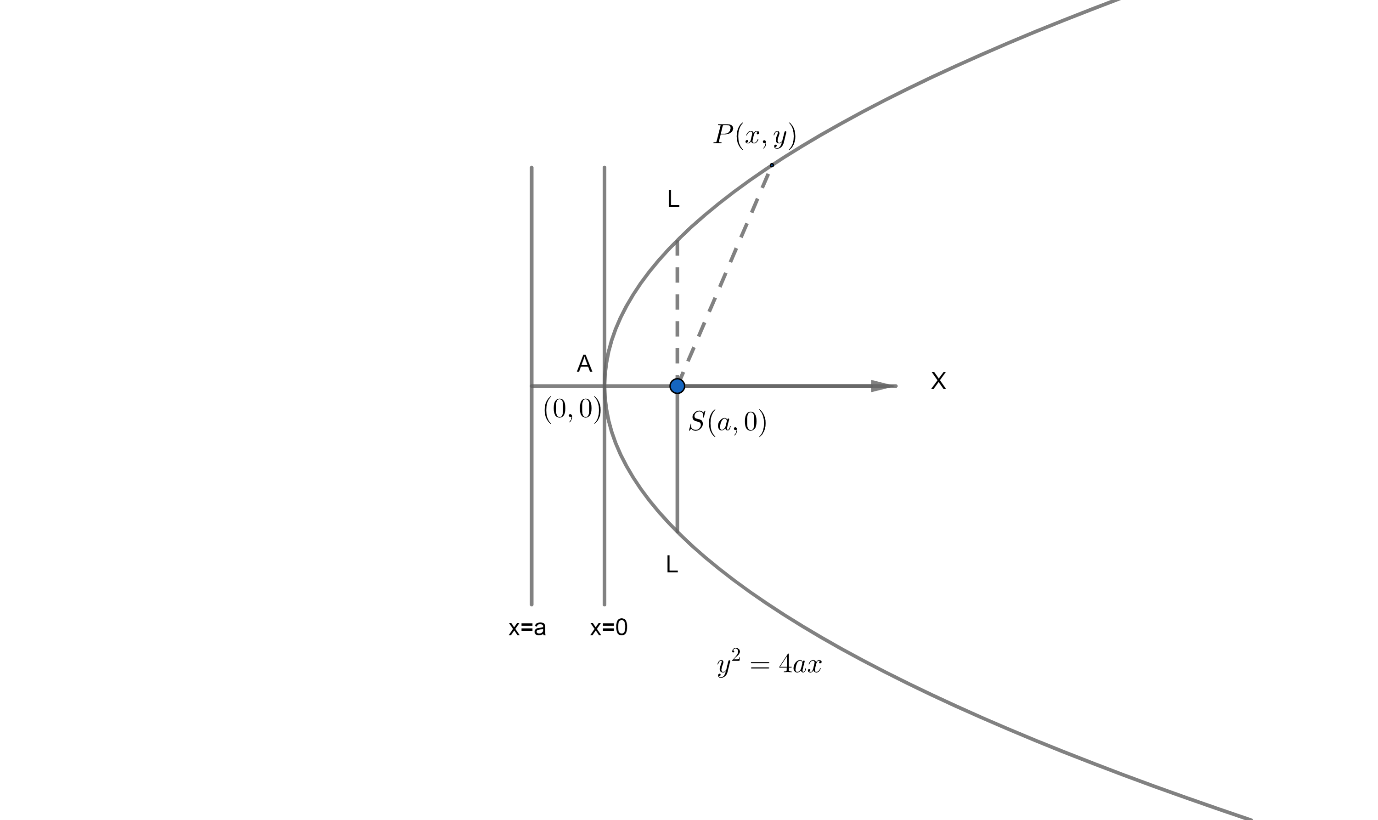
The point $P$ of parabola represent the parametric coordinates $\left( a{{t}^{2}},2at \right)$
Here, Vertex $=A\left( 0,0 \right)$
Focus $=S\left( a,0 \right)$
Equation of directrix $\Rightarrow x=-a$
Equation of axis $\Rightarrow y=0$
Length of Latus rectum $=4a$
Focal distance of Point $\left( x,y \right)=x+a$ .
Now substituting $\left( 3 \right)$ in $\left( 1 \right)$
\[\begin{align}
& {{\left( a{{t}^{2}} \right)}^{2}}+{{\left( 2at \right)}^{2}}+2g\left( a{{t}^{2}} \right)+2f\left( 2at \right)+c=0 \\
& \Rightarrow {{a}^{2}}{{t}^{4}}+\underline{4{{a}^{2}}{{t}^{2}}+2ga{{t}^{2}}}+4fat+c=0 \\
& {{a}^{2}}{{t}^{4}}+{{t}^{2}}\left( 4{{a}^{2}}+2ag \right)+4fat+c=0............\left( 4 \right) \\
\end{align}\]
Let us consider the roots of $4$ points where circle and parabola meets as ${{t}_{1,}}{{t}_{2,}}{{t}_{3,}}{{t}_{p}}.$
The sum of roots is always equal to zero.
i.e. \[{{t}_{1}}+{{t}_{2}}+{{t}_{3}}+{{t}_{4}}=0\]
point $1\left( a{{t}_{1}}^{2},2a{{t}_{1}} \right)$ ; point $2\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)$
point $3\left( a{{t}_{3}}^{2},2a{{t}_{3}} \right)$; point $4\left( a{{t}_{4}}^{2},2a{{t}_{4}} \right)$
The sum of the ordinate of the point \[=2a\left( {{t}_{1}}+{{t}_{2}}+{{t}_{3}}+{{t}_{4}} \right)\]
(i.e. $y-ordinate$ )$=2a\times 0=0$
Now, let us find the slope of points $1$ and $2$ , the points are $\left( a{{t}_{1}}^{2},2a{{t}_{1}} \right)$ and $\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)$
Slope $=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\Rightarrow $ Formula to find slope
$\therefore $ slope of point $1$ and $2$$=\left| \dfrac{2a{{t}_{2}}-2a{{t}_{1}}}{a{{t}_{2}}^{2}-a{{t}_{1}}^{2}} \right|$
By simplifying this, ${{a}^{2}}-{{b}^{2}}=\left( a-b \right)\left( a+b \right)$
\[\left| \dfrac{2a\left( {{t}_{2}}-{{t}_{1}} \right)}{a({{t}_{2}}^{2}-{{t}_{1}}^{2})} \right|=\left| \dfrac{2{a}{\left( {{t}_{2}}-{{t}_{1}} \right)}}{{a}{\left( {{t}_{2}}-{{t}_{1}} \right)}\left( {{t}_{2}}+{{t}_{1}} \right)} \right|\]
Cancel out the like terms on the above equation
$\therefore $ slope $=\left| \dfrac{2}{{{t}_{2}}+{{t}_{1}}} \right|..........\left( 5 \right)$
Similarly the slope of other two points $3$ and $4$
i.e., $\left( a{{t}_{3}}^{2},2a{{t}_{3}} \right)$ and $\left( a{{t}_{4}}^{2},2at4 \right)=\left| \dfrac{2}{{{t}_{3}}+{{t}_{4}}} \right|...........\left( 6 \right)$
Now equate $\left( 5 \right)=\left( 6 \right)$
$\left| \dfrac{2}{{{t}_{1}}+{{t}_{2}}} \right|=\left| \dfrac{2}{{{t}_{3}}+{{t}_{4}}} \right|\Rightarrow \dfrac{2}{{{t}_{1}}+{{t}_{2}}}=-\left( \dfrac{2}{{{t}_{3}}+{{t}_{4}}} \right)$
By simplifying the equation
${{t}_{3}}+{{t}_{4}}=-\left( {{t}_{1}}+{{t}_{2}} \right)$
$\Rightarrow {{t}_{1}}+{{t}_{2}}+{{t}_{3}}+{{t}_{4}}=0$ , this was proved earlier
$\therefore $ The lines are equally inclined to the axis.

Note: From both the first set and second set of the question, we need to prove that the sums of roots of coordinate are zero, i.e., ${{t}_{1}}+{{t}_{2}}+{{t}_{3}}+{{t}_{4}}=0$