
A circle has a radius of
Answer
403.5k+ views
Hint: We are given the radius of a circle and we need to find the circumference of the circle. Circumference of the circle is basically defined as the perimeter of the circle. To find the circumference of the circle, we use the formula
Complete step by step answer:
We are given the radius of the circle to be equal to
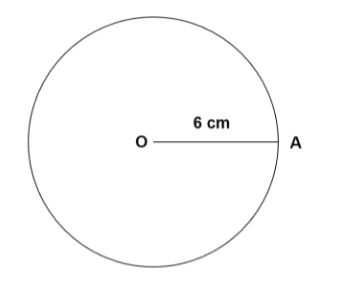
Here
Circumference of the circle
Now, since radius is equal to
Now, putting the value of
Opening the brackets, we get
As we know, Multiplication is associative, we can reshuffle the terms and get
Solving the above numeric value, we get
Now, putting the value of
Multiplying the above number, we get
Hence, when the radius of the circle is
Note: First of all, we must be very clear with the terminology used for different shapes just like in this question, circumference of the circle is basically the perimeter of the circle. Note that, Area of the circle is given by the formula
Complete step by step answer:
We are given the radius of the circle to be equal to

Here
Circumference of the circle
Now, since radius is equal to
Now, putting the value of
Opening the brackets, we get
As we know, Multiplication is associative, we can reshuffle the terms and get
Solving the above numeric value, we get
Now, putting the value of
Multiplying the above number, we get
Hence, when the radius of the circle is
Note: First of all, we must be very clear with the terminology used for different shapes just like in this question, circumference of the circle is basically the perimeter of the circle. Note that, Area of the circle is given by the formula
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Questions & Answers - Ask your doubts

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Science: Engaging Questions & Answers for Success

Trending doubts
List some examples of Rabi and Kharif crops class 8 biology CBSE

What is the feminine gender of a stag class 8 english CBSE

Write five sentences about Earth class 8 biology CBSE

Summary of the poem Where the Mind is Without Fear class 8 english CBSE

How many ten lakhs are in one crore-class-8-maths-CBSE

Advantages and disadvantages of science




