
. A circle is inscribed in trapezoid PQRS. If PS = QR = 25 cm, PQ = 18 cm and SR = 32 cm, what is the length of the diameter of the circle?
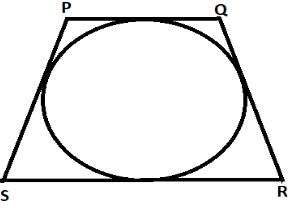

Answer
491.4k+ views
Hint: From the given dimensions we can see the two non-parallel sides are equal, the perpendicular when dropped will form a square and two equal right angles triangles (as angles of a square are 90°) ,then using geometry and Pythagoras theorem, we can find the length of the diameter.
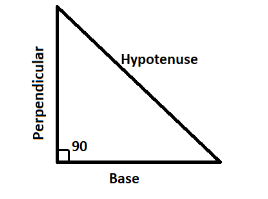
H = Hypotenuse
P= Perpendicular
B = Base
Of the right angle triangle.
Complete step-by-step answer:
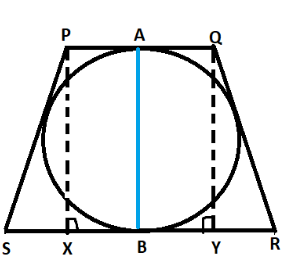
The length of the sides of this trapezoid are given:
PS = QR = 25 cm
PQ = 18 cm
SR = 32 cm
Let AB be the diameter of the circle inside the trapezoid.
As two non-parallel sides of this trapezoid (PS and QR) are equal, this is an isosceles trapezoid.
If we will drop perpendiculars from P and Q, the resultant figure will be a square say
PXYQ.
It can be seen that the lines PX, AB and QY are all equal:
PX = AB = QY ________ (1)
The angles of a square are of measure 90°, thus the formed triangles PSX and QYR are right angled triangles.
We can apply Pythagoras theorem on right angled triangle PSX to calculate the length of PX which in turn will provide the length of diameter AB
In
Hypotenuse (H) = PS
Perpendicular (P) = PX
Base (B) = SX
Now,
PQ = XY (sides of a square)
SX = RY (sides intercept equally on both the ends)
From the figure:
SR = XY + 2 SX (as SX = RY and we need the value of SX so we will consider that)
SX =
Substituting the values:
SX = 7 and
PS = 25 (given)
Substituting these values in (2) to calculate the value of PX, we get:
Taking square root both the sides, we get:
PX = 24 cm
From (1)
PX = AB
Therefore, the length of the diameter of the circle in the given figure is 24 cm.
Note: Right angle represents the angle of measure 90° and Pythagoras can be applied on right angled triangles only. Remember:
Trapezoid is also called as trapezium and its different types are:
Right: Having a pair of right angles
Isosceles: Two non-parallel sides equal in length
Scalene: Neither angles nor sides are equal.
H = Hypotenuse
P= Perpendicular
B = Base
Of the right angle triangle.
Complete step-by-step answer:

The length of the sides of this trapezoid are given:
PS = QR = 25 cm
PQ = 18 cm
SR = 32 cm
Let AB be the diameter of the circle inside the trapezoid.
As two non-parallel sides of this trapezoid (PS and QR) are equal, this is an isosceles trapezoid.
If we will drop perpendiculars from P and Q, the resultant figure will be a square say
PXYQ.
It can be seen that the lines PX, AB and QY are all equal:
PX = AB = QY ________ (1)
The angles of a square are of measure 90°, thus the formed triangles PSX and QYR are right angled triangles.
We can apply Pythagoras theorem on right angled triangle PSX to calculate the length of PX which in turn will provide the length of diameter AB
In
Hypotenuse (H) = PS
Perpendicular (P) = PX
Base (B) = SX
Now,
PQ = XY (sides of a square)
SX = RY (sides intercept equally on both the ends)
From the figure:
SR = XY + 2 SX (as SX = RY and we need the value of SX so we will consider that)
SX =
Substituting the values:
SX = 7 and
PS = 25 (given)
Substituting these values in (2) to calculate the value of PX, we get:
Taking square root both the sides, we get:
PX = 24 cm
From (1)
PX = AB
Therefore, the length of the diameter of the circle in the given figure is 24 cm.
Note: Right angle represents the angle of measure 90° and Pythagoras can be applied on right angled triangles only. Remember:

Trapezoid is also called as trapezium and its different types are:
Right: Having a pair of right angles
Isosceles: Two non-parallel sides equal in length
Scalene: Neither angles nor sides are equal.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 4 Maths: Engaging Questions & Answers for Success

Master Class 4 English: Engaging Questions & Answers for Success

Trending doubts
The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

What is the difference between Atleast and Atmost in class 9 maths CBSE

Choose the antonym of the word given below Furious class 9 english CBSE

What comes after 10 crore in Indian system class 9 maths CBSE

What is the full form of pH?

Who is eligible for RTE class 9 social science CBSE




