Question

A circle touching x-axis at (3,0) and making an intercept of length 8 on the y-axis passes through the point
$\begin{align}
  & \left( A \right)\left( 3,10 \right) \\
 & \left( B \right)\left( 2,3 \right) \\
 & \left( C \right)\left( 1,5 \right) \\
 & \left( D \right)\left( 3,5 \right) \\
\end{align}$

Answer 1

Hint: We solve this question by assuming the radius of the circle as r and then we find the centre of the circle as it touches the x-axis centre of the circle becomes (3,r). Then we consider the right-angled triangle and apply Pythagoras theorem and we can find the radius of the circle by solving it. Thereby we can find the points lying on the circle.

Complete step by step answer:
We are given that our circle touches x-axis at (3,0) and the circle makes an intercept of length 8 on the y-axis.

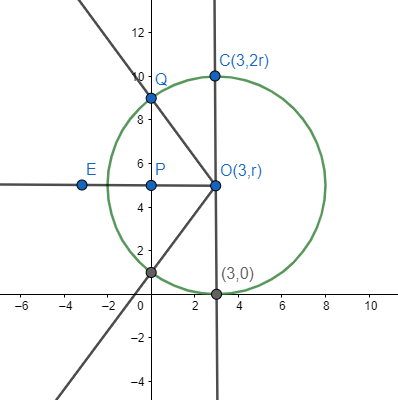
Let us look at the figure drawn based on given information.
Let us assume the radius of the given circle as r. As the circle touches the x-axis, it is a tangent to the circle and so a line drawn from the centre of the circle to (3,0) is perpendicular to the x-axis. As we assumed the radius as r, our centre becomes $O\left( 3,r \right)$.
Now let us draw a perpendicular from centre to the y-axis. As a perpendicular line from centre to a secant to the circle bisects the secant, point P is the midpoint of the intercept made by the circle on the y-axis.
Now, consider the triangle $\Delta OPQ$. As it is a right-angled triangle, we can apply Pythagoras theorem on this triangle.
Let us consider the Pythagoras theorem,
Sum of squares of sides is equal to the square of the hypotenuse, that is ${{a}^{2}}+{{b}^{2}}={{c}^{2}}$.
Using the above formula, we get
$\begin{align}
  & \Rightarrow O{{P}^{2}}+P{{Q}^{2}}=O{{Q}^{2}} \\
 & \Rightarrow {{3}^{2}}+{{4}^{2}}={{r}^{2}} \\
 & \Rightarrow 9+16={{r}^{2}} \\
 & \Rightarrow {{r}^{2}}=25 \\
 & \Rightarrow r=5 \\
\end{align}$
So, we get the radius of the circle as 5 units.
As we got the radius r=5 units, we can see that the point C becomes
$\Rightarrow \left( 3,2r \right)=\left( 3,2\times 5 \right)=\left( 3,10 \right)$
Which is the same as the point in Option A.

So, the correct answer is “Option A”.

Note: We can also solve the problem by finding the equation of the circle. As we obtained the r value as 5, the centre of the circle becomes (3,5) and radius is equal to 5.
So, let us find the equation of the circle.
$\begin{align}
  & \Rightarrow {{\left( x-3 \right)}^{2}}+{{\left( y-5 \right)}^{2}}=25 \\
 & \Rightarrow {{x}^{2}}-6x+9+{{y}^{2}}-10y+25=25 \\
 & \Rightarrow {{x}^{2}}-6x+9+{{y}^{2}}-10y=0 \\
 & \Rightarrow {{x}^{2}}+{{y}^{2}}-6x-10y+9=0 \\
\end{align}$
So, the equation of the given circle is ${{x}^{2}}+{{y}^{2}}-6x-10y+9=0$.
Then we substitute the given options in the above equation to find which of them lies on the circle. Thereby we can find the answer.