Question

A circular curve of highway is designed for traffic moving at \[92\dfrac{{km}}{h}\], when assumed the traffic consists of cars without negative lift.
(a) If the radius of the curve is $150m$, what is the correct angle of banking of the road?
(b) If the curve were not banked, what would be the minimum coefficient of friction between tires and road that would keep traffic from skidding out of the turn when travelling at \[92\dfrac{{km}}{h}\]?

Answer 1

Hint: In order to solve this question, we will first equate the force equation in the $x$ direction and the $y$ direction, then we will take the coefficient of friction equal to zero as this is the worst case and take the ratio of the two equations. To solve the second part of this question, we will apply the condition in which the curve is not banked.

Complete step by step answer:
Let $mg$ be the weight of car which is travelling, let $r$ be the radius of curve, let $\theta $ be the angle of banking of the road, let $v$ be the maximum velocity of the car with which it can travel safely while it negotiates the curve, let $N$ be the normal reaction, and let ${\mu _s}$ be the coefficient of friction which is acting between the road and its tyres.

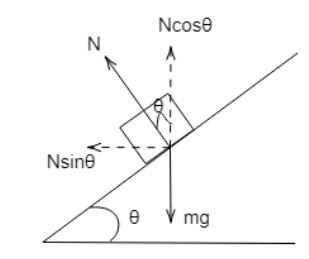
(a) The centripetal force acting on a body undergoing circular motion $ = \dfrac{{m{v^2}}}{r}$
Also, the friction acting between the tyre and the road is $f = {\mu _s}N$
Now, let us assume that the car is present at the origin.
So, the force equations acting for the maximum velocity are:
$\dfrac{{m{v^2}}}{r} = N\sin \theta + {\mu _s}N\cos \theta $
Also, $mg + {\mu _s}N\sin \theta = N\cos \theta $
The worst case for the banking of roads is consider when ${\mu _s} = 0$
This is done in order to tackle the slippery road in the rainy season.
Putting ${\mu _s} = 0$ in the above two equations, we get,
$\dfrac{{m{v^2}}}{r} = N\sin \theta .......(1)$
$\Rightarrow mg = N\cos \theta ......(2)$

On dividing equation (1) with equation(2), we get,
$\dfrac{{\dfrac{{m{v^2}}}{r}}}{{mg}} = \dfrac{{N\sin \theta }}{{N\cos \theta }}$
On further solving this,
$\tan \theta = \dfrac{{{v^2}}}{{rg}}.......(3)$
In this question, we are given,
$v = 92\dfrac{{km}}{h}$
On converting it into metre per second, we get,
$v = 25.5\dfrac{m}{s}$
Also, $r = 150m$ and $g = 9.81\dfrac{m}{{{s^2}}}$
On putting these values in equation (3), we get,
$\tan \theta = {\dfrac{{\left( {25.5} \right)}}{{150 \times 9.81}}^2}$
$\Rightarrow \tan \theta = 0.44382$
On applying the concept of inverse trigonometric function, we get,
$\therefore \theta = {23.9^o}$

(b) If the curves of the road are not banked, then this means that $\theta = {0^ \circ }$
So, $\sin \theta = 0$ and $\cos \theta = 1$
So, the equation (1) and equation (2) will take the form,
$\dfrac{{m{v^2}}}{r} = {\mu _s}N......(4)$
$\Rightarrow mg = N.......(5)$
On putting the value of $N$ from equation (5) in equation (1) and further solving to get the minimum coefficient of friction required to prevent the car from skidding off the road,
$\dfrac{{m{v^2}}}{r} = {\mu _{s(\min )}}mg$

On cancelling $m$ on both the sides,
$\dfrac{{{v^2}}}{r} = {\mu _{s(\min )}}g$
\[\Rightarrow {\mu _{s(\min )}} = \dfrac{{{v^2}}}{{rg}}\]
Now, this is equal to the expression of $\tan \theta $ that we got in the part (a) of the question. So,
$\therefore {\mu _{s(\min )}} = 0.44382$
So, the angle of banking of the road is $\theta = {23.9^o}$. Also, the minimum coefficient of friction between the tyre and the road is ${\mu _{s(\min )}} = 0.44382$.

Note: The static friction depends on the magnitude of the force which is being applied while the kinetic friction does not depend on the magnitude of the force which is being applied. Static friction opposes the start of motion of a body whereas kinetic friction is the opposition which is offered to a body which is already in motion.