Question

A circular park has a path of uniform width around it. The difference between outer and inner circumference of the circular path is 132m. Its width is: Take $\left( {\pi = \dfrac{{22}}{7}} \right)$.

A.22m
B.20m
C.21m
D.24m

Answer 1

Hint: We can find the circumference of the inner and outer circle using the equation $C = 2\pi r$ . Then we can find their difference and equate it to the given value. Then by further simplification, we can find the difference in their radius. The width of the path is also given by the difference in the radii.

Complete step-by-step answer:
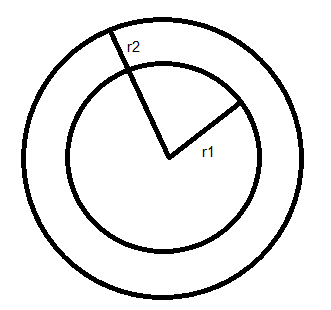
We have the radius of the outer circle as ${r_1}$
We know that the circumference of a circle with radius r is given by, $C = 2\pi r$
So, the circumference of the outer circle is given by,
 ${C_1} = 2 \times \pi \times {r_1}$
Now we can consider the inner circle.
We have its radius as ${r_2}$ .
Then its circumference is given by,
 ${C_2} = 2 \times \pi \times {r_2}$
Now we can find the difference between the outer and inner circumferences.
 $ \Rightarrow {C_2} - {C_1} = 2 \times \pi \times {r_2} - 2 \times \pi \times {r_1}$
We can take the common factors outside,
 $ \Rightarrow {C_2} - {C_1} = 2 \times \pi \times \left( {{r_2} - {r_1}} \right)$ … (1)
It is given that the difference between outer and inner circumference of the circular path is 132m.
 $ \Rightarrow {C_2} - {C_1} = 132m$ … (2)
On equating equations (1) and (2), we get,
 $ \Rightarrow 2 \times \pi \times \left( {{r_2} - {r_1}} \right) = 132$
On rearranging, we get,
 $ \Rightarrow \left( {{r_2} - {r_1}} \right) = \dfrac{{132}}{{2 \times \pi }}$
On substituting $\pi = \dfrac{{22}}{7}$ , we get,
 $ \Rightarrow \left( {{r_2} - {r_1}} \right) = \dfrac{{132 \times 7}}{{2 \times 22}}$
On simplification, we get,
 $ \Rightarrow \left( {{r_2} - {r_1}} \right) = 21$ … (3)
From the figure, the width of the path is given by subtracting the radius of the inner circle from the radius of the outer circle.
Thus from (3) the difference between their radii is, $\left( {{r_2} - {r_1}} \right) = 21$
Therefore, the width of the path is given 21m
So the correct answer is option C.

Note: We do not need to find the values of each radii. We just need only the difference between the radius. As we are asked to use the value of $\pi = \dfrac{{22}}{7}$ , we must only use this to get the exact width as given in the options. If we take other values of $\pi $ , we may get a decimal value that does not match with the given option. If the value of $\pi $ is not given, then we may take the decimal value of $\pi $ and obtain a decimal as the width of the path. Then we can round off the decimal to get the correct option.