
A closed cylinder has volume
Answer
417k+ views
Hint: In order to solve this question, the basic knowledge about a cylinder and it’s standard formulae is required. A cylinder is a three dimensional solid shape consisting of two parallel circular shaped bases ( always congruent and parallel to each other ) which are joined by a curved surface. The basic formulae for a cylinder having radius r and height h is given by
Complete step-by-step solution:
The basic diagram for a cylinder is shown below;
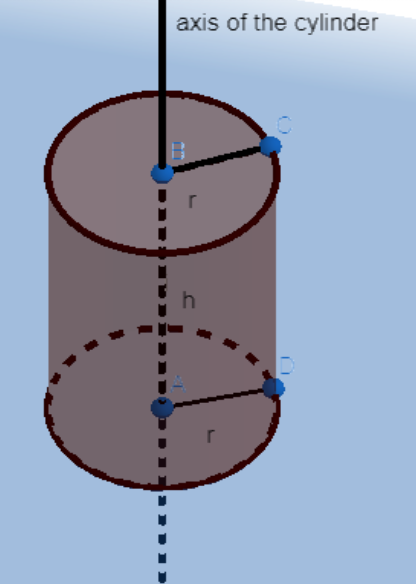
Figure : Three dimensional representation of a cylinder
According to the question;
Given : Volume of cylinder
By the formula stated above for the volume of a cylinder, we can equate;
We can calculate the expression for the height of the cylinder from the above equation as;
We know that the surface area of cylinder is given by;
Put the value of h in the above expression from equation
Multiplying
Differentiate the above equation with respect to the radius
Using the above standard differentiation rule;
Equating equation
Further solving the above equation ;
Rearranging the above equation;
Therefore, we get the value of radius as ;
We can further simplify for the value of radius by putting
On further simplification;
Therefore,
Differentiating equation
Therefore, we get the equation for the double derivative as ;
From equation
Therefore , this is the point of minima with critical point
Hence, we can say that the radius of the base must be
So, the correct answer for this question is
Note: To calculate maxima or minima for a given function, there are certain steps which need to be followed:
Complete step-by-step solution:
The basic diagram for a cylinder is shown below;

Figure : Three dimensional representation of a cylinder
According to the question;
Given : Volume of cylinder
By the formula stated above for the volume of a cylinder, we can equate;
We can calculate the expression for the height of the cylinder from the above equation as;
We know that the surface area of cylinder is given by;
Put the value of h in the above expression from equation
Multiplying
Differentiate the above equation with respect to the radius
Using the above standard differentiation rule;
Equating equation
Further solving the above equation ;
Rearranging the above equation;
Therefore, we get the value of radius as ;
We can further simplify for the value of radius by putting
On further simplification;
Therefore,
Differentiating equation
Therefore, we get the equation for the double derivative as ;
From equation
Therefore , this is the point of minima with critical point
Hence, we can say that the radius of the base must be
So, the correct answer for this question is
Note: To calculate maxima or minima for a given function, there are certain steps which need to be followed:
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Questions & Answers - Ask your doubts

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Science: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the full form of POSCO class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE

How do you prove that the diagonals of a rectangle class 10 maths CBSE




