Question

A compound AB has simple cubic structure and has molecular mass 99. Its density is 3.4 $gc{m^{ - 3}}$. What will be the edge of the unit cell?

Answer 1

Hint: The unit cell of a crystal is the smallest unit of the crystal lattice, a representation of three dimensional pattern of the entire crystal. As per assumptions, it is considered that in a crystal the same unit cell is repeated over and over again. The unit cell has opposite and parallel faces. The edge of a unit cell is connected to equivalent points. The unit cells are categorised into 7 categories, based on internal angles and edge lengths of the unit cell. The cubic lattice is one of the categories of unit cells.

Formula Used: The edge of unit cell can be determined by using following formula:
$[{a^3} = \dfrac{{Z \times M}}{{e \times {N_A}}}]$
Here is the length of the edge of the unit cell. The letter Z represents the number of molecules per unit cell and M is the molar mass of the molecule. The density of the compound is e and ${N_A}$ is Avogadro's number.

Complete step-by-step answer:
As given, the compound AB has simple cubic structure. The simple cubic unit cell has the lattice points present only at its corners. The simple cubic lattice unit cells are the smallest repetitive unit. The lattice point present at the corners are useful for ions, metals or molecules to have a crystalline structure. In simple cubic lattice, each unit cell is identical due to the fact that edges of each unit cell are equidistant. The unit cell in simple cubic lattice will have only one atom.
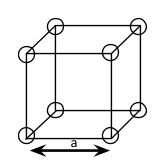
The given diagram shows a simple cubic lattice with lattice point only at its corners.

Step 1: First we need to obtain a formula for calculating the length of edge of the unit cell.

Density of unit cell $(e) = \dfrac{{Mass\,of\,unit\,cell\,(m)}}{{Volume\,of\,unit\,cell\,(V)}}$…………………(1)
We know that, $Mass\,of\,unit\,cell\,(m) = number{\text{ of atoms in unit cell(z)}} \times {\text{mass of each atom(m)}}$……(2)
But, ${\text{mass of each an atom(m) = }}\dfrac{M}{{{N_A}}}$………………….(3)
Here, M is the molar mass and ${N_A}$ is Avogadro's number.
Also, $Volume\,of\,unit\,cell\,(V) = {a^3}$……………………..(4)
From formula (1) to (4), we know that
$e = \dfrac{m}{V} = \dfrac{{z \times M}}{{{a^3} \times {N_A}}}$ ……………………………………………..(5)
If we rearrange the formula (5), we get
\[{a^3} = \dfrac{{Z \times M}}{{e \times {N_A}}}\]……………….(6)
Step 2: We have got the formula for finding out the edge of the unit cell of the simple cubic structure of compound AB.
For a simple cubic structure, $[Z = 1]$
The Avogadro’s number, ${N_A} = 6.023 \times {10^{23}}$
The molar mass of compound AB, $M = 99$
The density of unit cell, $e = 3.4g {cm^{ - 3}}$
Let us substitute the respective values in formula 6 to obtain the value of $[{a^3}]$.
$[{a^3} = \dfrac{{Z \times M}}{{e \times {N_A}}}]$
${a^3} = \dfrac{{1 \times 99}}{{3.4 \times 6.023 \times {{10}^{23}}}}$
${a^3} = 4.8344 \times {10^{ - 23}}\,c{m^3}$
We have to take the cubic root of the above value to obtain the value of a.
$\therefore a = {(4.8344 \times {10^{23}})^{1/3}}cm$
$a = 3.64 \times {10^{ - 8}}cm = 3.64 \times {10^{ - 10}}m$
$\therefore a = 8.64{{\buildrel _{\circ} \over {\mathrm{A}}}}$ $(\because 1{{\buildrel _{\circ} \over {\mathrm{A}}}} = {10^{ - 10}}m)$

Hence, the edge of the unit cell of cubic structure of compound AB is $3.64{{\buildrel _{\circ} \over {\mathrm{A}}}}$.

Note:
-The simple cubic unit cell is a primitive cell that means the unit cell will have only one lattice point. -The number of Z that is the number of atoms present in a unit cell is 1. Hence, we have taken the value of Z as 1.
-The symbol, S${{\buildrel _{\circ} \over {\mathrm{A}}}}$ represents angstrom which is a metric unit of length and it equals to that of ${10^{ - 10}}m$.
-Also, remember that the formula for density of a unit cell will provide us with the value of ${a^3}$. We have to take the cubic root of ${a^3}$, in order to obtain the correct value for the length of the edge of the unit cell.