Question

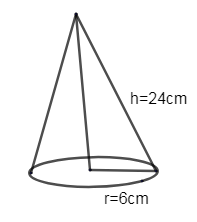
A cone of height 24cm and radius of base 6cm is made up of modelling clay. A child moulds it in the form of a sphere. Find the radius of the sphere.

Answer 1

Hint: The cone is remodelled into the shape of a sphere. So the volume of the cone and sphere will be the same. Find the volume of the cone and equate it to the volume of the sphere to get the radius of the sphere.

Complete step-by-step answer:
It is given that a child reshapes cones into a sphere. Thus the volume will remain the same.

\[\therefore \]Volume of cone = volume of the sphere.
First we need to find the volume of cones.
Given that height of cone, h = 24cm.
Similarly, radius r of the cone, r = 6cm.
We know that the volume of cones is given by \[\dfrac{1}{3}\pi {{r}^{2}}h\].
\[\therefore \]Volume of cone = \[\dfrac{1}{3}\pi {{r}^{2}}h\].
Substitute the values of r and h in the equation of volume of cone.

\[\therefore \]Volume of cone \[=\dfrac{1}{3}\pi \times {{6}^{2}}\times 24\] [Take, \[\pi =\dfrac{22}{7}\]]
                                  \[\begin{align}
 & =\dfrac{1}{3}\times \dfrac{22}{7}\times 6\times 6\times 24 \\
 & =288\pi c{{m}^{3}} \\
\end{align}\]

Now the cone is reshaped to a sphere. Let the radius of the sphere be taken as r.
Thus we know, volume of sphere = \[\dfrac{4}{3}\pi {{r}^{3}}\].
We said that, volume of cone = volume of sphere.
\[\therefore \dfrac{4}{3}\pi {{r}^{3}}=288\pi \]
Cancel out like terms and cross multiply.
\[{{r}^{3}}=\dfrac{288\times 3}{4}=72\times 3\]
\[r=\sqrt[3]{216}\], (take the cube root)
\[r=\sqrt[3]{6\times 6\times 6}\]= 6cm.
Hence, we got the radius of the sphere as 6cm.

Note: Here the same quantity of material is used to reshape cones to sphere. So we can make out that their volume will be the same irrespective of their height and radius. Remember the equation of volumes of cone and sphere.