Question

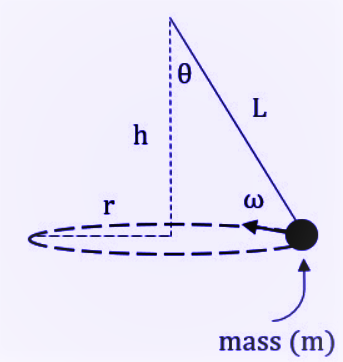
A conical pendulum is in a circle with angular velocity ω as shown. If tension in the string is T, which of the following are correct?

A $T = m{w^2}I$
B. $T = mg\cos \theta $
C. $T\sin \theta = m{w^2}I$
D.$T = m{w^2}I\sin \theta $

Answer 1

Hint: In order to solve this numerical we need to understand the free body diagram. After this, we need to know how to balance the net force acting on the object. Then we can find the tension force in the string.

Complete step by step answer:

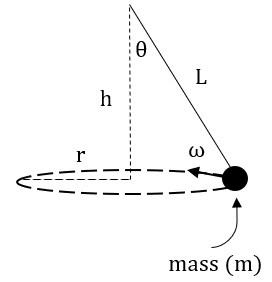
From the above diagram
The centripetal force is given by= $\dfrac{{m{v^2}}}{r}$
The tension string can be resolved into two components. Therefore the horizontal component is taken as $\sin \theta $.
The tension force due to the string which is given by
$T = \dfrac{{m{v^2}\sin \theta }}{I}$
We know that the relation between the linear velocity and angular velocity formula is given by
$v = \omega I$…….. (1)
Substitute equation (1) in above formula is given by
$T = \dfrac{{m{\omega ^2}{I^2}\sin \theta }}{I}$
$\implies T = m{\omega ^2}I\sin \theta $

So, the correct answer is “Option D”.

Note:
While solving this type of problem we need to be very careful about the direction of forces. If only one force acting in the same direction should be balanced by another force. Students should not confuse with the centripetal and centrifugal forces. Centripetal force is force acting towards and centrifugal is the force away from the center.