
A conical vessel of radius 6cm and height 8 cm is completely filled with water. A sphere is lowered into the water and its size is such that when it touches the sides it is just immersed. What fraction of water overflows?
Answer
439k+ views
Hint: When the sphere just touches the inner surface of the cone, then the surface of the cone is nothing but a tangent to the sphere. Also, the centre of the sphere is R distance below the surface of the base of the cone (Where R is the radius of the sphere)
The volume of a sphere is
(Where ‘r ‘ is the radius of the sphere)
The volume of a cone is
(Where ‘r’ is the radius of the cone and’ h’ is the height of the cone)
Complete step-by-step answer:
As mentioned in the question, the sphere is completely immersed in the cone.
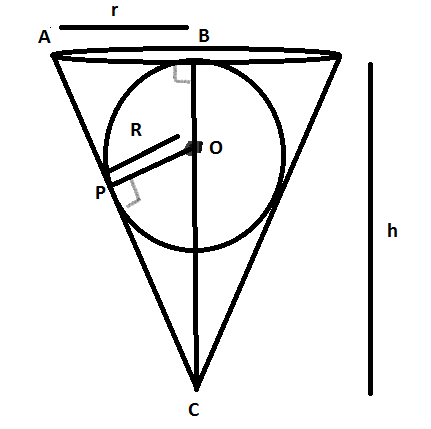
Now, by referring to the figure, we can say that
Now, if
Now, on applying sin formula in
(Where R is the radius of the sphere)
Therefore, using the formula for finding the volume of a sphere as it is given in the hint, we get
Now, the fraction of water which overflows is given as follows
Hence, the fraction of water that overflows is
Note: The students can make an error if they don’t know the formulas for volume of sphere and cone and also the trigonometric ratio which are given in hint as
The volume of a sphere is
(Where ‘r ‘ is the radius of the sphere)
The volume of a cone is
(where ‘r’ is the radius of the cone and’ h’ is the height of the cone)
The volume of a sphere is
(Where ‘r ‘ is the radius of the sphere)
The volume of a cone is
(Where ‘r’ is the radius of the cone and’ h’ is the height of the cone)
Complete step-by-step answer:
As mentioned in the question, the sphere is completely immersed in the cone.

Now, by referring to the figure, we can say that
Now, if
Now, on applying sin formula in
(Where R is the radius of the sphere)
Therefore, using the formula for finding the volume of a sphere as it is given in the hint, we get
Now, the fraction of water which overflows is given as follows
Hence, the fraction of water that overflows is
Note: The students can make an error if they don’t know the formulas for volume of sphere and cone and also the trigonometric ratio which are given in hint as
The volume of a sphere is
(Where ‘r ‘ is the radius of the sphere)
The volume of a cone is
(where ‘r’ is the radius of the cone and’ h’ is the height of the cone)
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Trending doubts
The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

Chandigarh is the capital of A Punjab B Haryana C Punjab class 10 social science CBSE

What is the past participle of wear Is it worn or class 10 english CBSE

What is the full form of POSCO class 10 social science CBSE

How fast is 60 miles per hour in kilometres per ho class 10 maths CBSE

Choose the feminine form of the given noun Fox AFoxess class 10 english CBSE




