
A constant function is a periodic function.
A. True
B. False
Answer
495k+ views
Hint: We need to check whether the given statement is true or false. A periodic function can be defined as a function returning to the same value at regular intervals. A function
Complete step by step answer:
We need to check whether the statement “ a constant function is a periodic function” is true or false.
Let us see what a periodic function is.
A periodic function can be defined as a function returning to the same value at regular intervals.
For example,
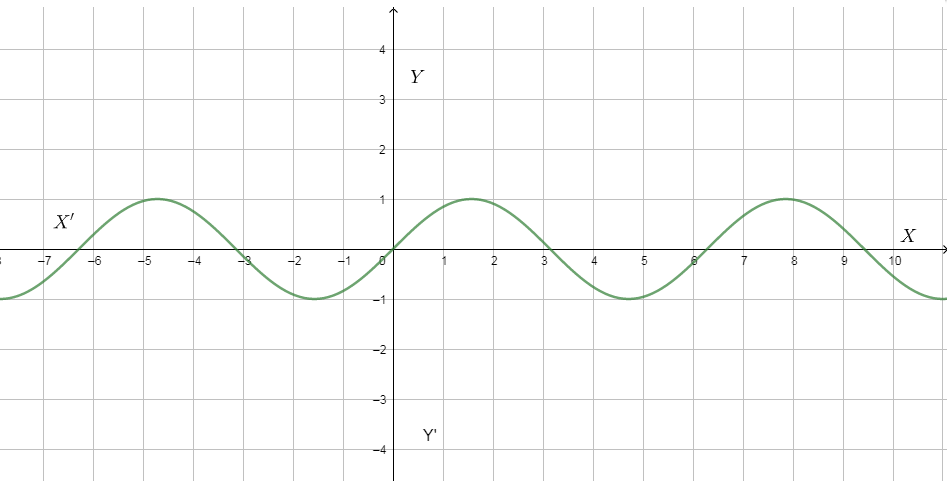
The function repeats continuously in a similar fashion. For example, from the figure, the wave begins from 0 to 3 goes to the negative part from 3 to 6. This fashion is repeated again.
A function
Constant function a real-valued function of a real-valued argument, denoted by
The below figure shows the graph of constant function
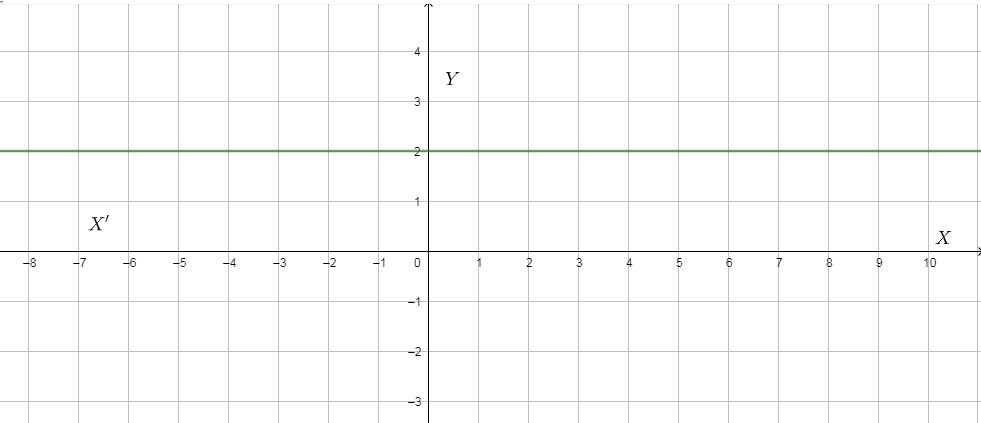
Hence, a constant function is a periodic function with a period
Hence, the given statement is True.
Note:
All constant functions are periodic irrespective of its type, that is, whether it is an integer, a fraction, or real number.
Complete step by step answer:
We need to check whether the statement “ a constant function is a periodic function” is true or false.
Let us see what a periodic function is.
A periodic function can be defined as a function returning to the same value at regular intervals.
For example,

The function repeats continuously in a similar fashion. For example, from the figure, the wave begins from 0 to 3 goes to the negative part from 3 to 6. This fashion is repeated again.
A function
Constant function a real-valued function of a real-valued argument, denoted by
The below figure shows the graph of constant function

Hence, a constant function is a periodic function with a period
Hence, the given statement is True.
Note:
All constant functions are periodic irrespective of its type, that is, whether it is an integer, a fraction, or real number.
Latest Vedantu courses for you
Grade 9 | CBSE | SCHOOL | English
Vedantu 9 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹37,300 per year
EMI starts from ₹3,108.34 per month
Recently Updated Pages
Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Chandigarh is the capital of A Punjab B Haryana C Punjab class 10 social science CBSE

What are the public facilities provided by the government? Also explain each facility




