
A constant function is a periodic function.
(a)true
(b)false
Answer
497.1k+ views
Hint: To solve this question we will first see the basic need of function to be periodic and then by the graph of a constant function, we will conclude that whether the constant function is periodic or not.
Before we solve this function let us see with example what periodic function is and what is the constant function with their properties.
Complete step-by-step solution:
A function f ( x ) who repeats it’s graph after a fixed interval is called a periodic function that is if we have a function f ( x ) and the period of the function f ( x ) is T then, f ( x ) = f ( x + T ).
Such smallest T is called the fundamental period of function f ( x )
Let us take an example of a periodic function.
Let function be f ( x ) = sinx.
We know that the graph of function
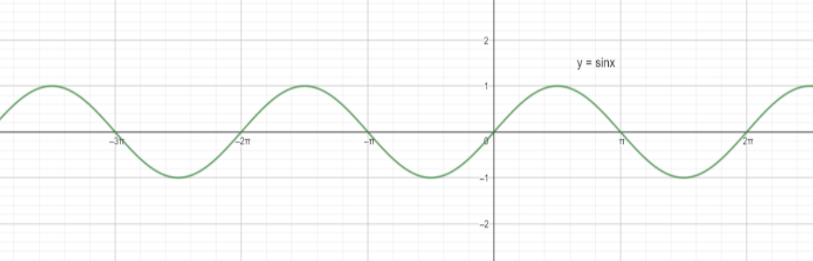
Now, from the graph, we can see that
So, we can say that period of
So, fundamental period of function sinx is
Now, a constant function is a function which gives the same output value for all its input value that is if we have a function f ( x ) and for all its domain x, we have the same output, say a or we have range = {a}, then the function is constant.
If we have function f ( x ) = a, then for all x, we will have the same output which is a.
The graph of a constant function is a straight line parallel to the x-axis or y-axis.
For example, let function be f ( x ) = 5, then whatever value we take for x, we will get output equals to 5 only.
The graph of f ( x ) = 5 will be parallel to the y-axis passing from point ( 0, 5 ).
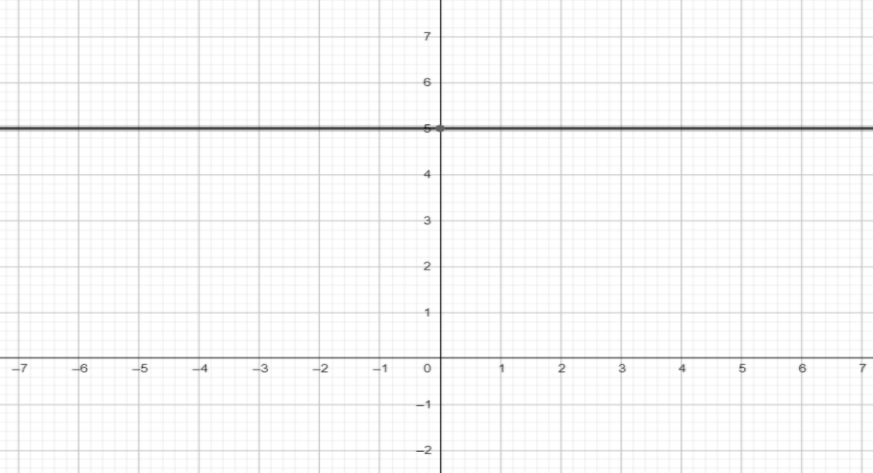
Now, as the function is having constant value, so constant function repeats it’s a graph for all x.
So, a constant function is a periodic function with no fundamental period as we cannot determine such a small T for constant function.
So, the statement is true.
Hence, option ( a ) is true.
Note: Always remember the definition and at least one or more examples of a periodic function with their fundamental period as it helps in solving questions and plotting graphs. Also, remember that if we have a function f ( x ) and for all its domain x, we have the same output, say a or we have range = {a}, then the function is constant and the graph of constant function is a straight line parallel to x-axis or y-axis.
Before we solve this function let us see with example what periodic function is and what is the constant function with their properties.
Complete step-by-step solution:
A function f ( x ) who repeats it’s graph after a fixed interval is called a periodic function that is if we have a function f ( x ) and the period of the function f ( x ) is T then, f ( x ) = f ( x + T ).
Such smallest T is called the fundamental period of function f ( x )
Let us take an example of a periodic function.
Let function be f ( x ) = sinx.
We know that the graph of function

Now, from the graph, we can see that
So, we can say that period of
So, fundamental period of function sinx is
Now, a constant function is a function which gives the same output value for all its input value that is if we have a function f ( x ) and for all its domain x, we have the same output, say a or we have range = {a}, then the function is constant.
If we have function f ( x ) = a, then for all x, we will have the same output which is a.
The graph of a constant function is a straight line parallel to the x-axis or y-axis.
For example, let function be f ( x ) = 5, then whatever value we take for x, we will get output equals to 5 only.
The graph of f ( x ) = 5 will be parallel to the y-axis passing from point ( 0, 5 ).

Now, as the function is having constant value, so constant function repeats it’s a graph for all x.
So, a constant function is a periodic function with no fundamental period as we cannot determine such a small T for constant function.
So, the statement is true.
Hence, option ( a ) is true.
Note: Always remember the definition and at least one or more examples of a periodic function with their fundamental period as it helps in solving questions and plotting graphs. Also, remember that if we have a function f ( x ) and for all its domain x, we have the same output, say a or we have range = {a}, then the function is constant and the graph of constant function is a straight line parallel to x-axis or y-axis.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




