Question

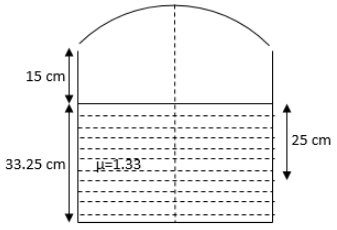
A container is filled with water (\[\mu = 1.33\]) upto a height of \[33.25\,{\text{cm}}\]. A concave mirror is placed \[15\,{\text{cm}}\] above the water level and an image of an object is placed at the bottom is formed \[25\,{\text{cm}}\] below the water level. The focal length of the mirror is

A. $10$
B. $15$
C. $20$
D. $25$

Answer 1

Hint:Use the expression for mirror formula. This formula gives the relation between focal length of mirror, object and image distance from the mirror. Determine the values of the given apparent distances in the water due to the water medium. Then substitute the values of object and image distance in the mirror formula.

Formulae used:
The mirror formula is given by
\[\dfrac{1}{f} = \dfrac{1}{u} + \dfrac{1}{v}\] …… (1)
Here, \[f\] is the focal length of the mirror, \[u\] is object distance from the mirror and \[v\] is image distance from the mirror.
The refractive index \[\mu \] of a medium is given by
\[\mu = \dfrac{{{\text{Real depth}}}}{{{\text{Apparent depth}}}}\] …… (2)

Complete step by step answer:
We have given that the height of the water with refractive index 1.33 from the bottom of the container is \[33.25\,{\text{cm}}\]. The distance of the concave mirror from the upper surface of the water is \[15\,{\text{cm}}\] and the image of the object at the bottom of the container is formed at a distance \[25\,{\text{cm}}\] from the upper water surface.

From the figure given, we can see that the actual distance of the object from the concave mirror is the sum of distances \[33.25\,{\text{cm}}\] and \[15\,{\text{cm}}\].
From the figure, we can also see that the distance of the image of object from the concave mirror is the sum of the distances \[15\,{\text{cm}}\] and \[25\,{\text{cm}}\].

But due to the water medium, the apparent object and image distances from the concave mirror are different which can be determined using equation (2).
The apparent object distance is
\[ \Rightarrow u = \dfrac{{33.25\,{\text{cm}}}}{{1.33}} + 15\,{\text{cm}}\]
\[ \Rightarrow u = 40\,{\text{cm}}\]
Therefore, the apparent object distance due to the water medium is \[40\,{\text{cm}}\].

The apparent image distance is
\[ \Rightarrow v = \dfrac{{25\,{\text{cm}}}}{{1.33}} + 15\,{\text{cm}}\]
\[ \Rightarrow v = 33.79\,{\text{cm}}\]
Therefore, the apparent image distance due to the water medium is \[33.79\,{\text{cm}}\].

We can now determine the focal length of the given concave mirror i=using equation (1).
Substitute \[ - 40\,{\text{cm}}\] for \[u\] and \[ - 33.79\,{\text{cm}}\] for \[v\] in equation (1).
\[\dfrac{1}{f} = \dfrac{1}{{ - 40\,{\text{cm}}}} + \dfrac{1}{{ - 33.79\,{\text{cm}}}}\]
\[ \Rightarrow \dfrac{1}{f} = \dfrac{{ - 33.79\,{\text{cm}} - 40\,{\text{cm}}}}{{\left( { - 40\,{\text{cm}}} \right)\left( { - 33.79\,{\text{cm}}} \right)}}\]
\[ \Rightarrow f = \dfrac{{\left( { - 40\,{\text{cm}}} \right)\left( { - 33.79\,{\text{cm}}} \right)}}{{ - 33.79\,{\text{cm}} - 40\,{\text{cm}}}}\]
\[ \Rightarrow f = \dfrac{{1351.6}}{{ - 73.79}}\]
\[ \Rightarrow f = - 18.31\,{\text{cm}}\]
\[ \therefore f = - 20\,{\text{cm}}\]

Therefore, the focal length of the given concave mirror is \[ - 20\,{\text{cm}}\]. Hence, the correct option is C.

Note:The students may directly substitute the values of object and image distance from the figure instead of determining the apparent distances. But this will not give the correct final answer. The signs of object distance, image distance and focal length are taken negative because for the concave mirror the distances in front of the mirror are taken negative and behind the mirror are taken positive.