Question

A converging beam of light travelling in air converges at a point as shown in the figure. When a glass sphere of refractive index 1.5 is introduced in between the path of the beam, calculate the position of the image. Also draw the ray diagram for the image formed.

Answer 1

Hint: The light rays will refract first at surface S and then at surface S’. Which means that 2 images are formed – one intermediate and one final. Use the formula $\dfrac{{{\mu }_{2}}}{v}-\dfrac{{{\mu }_{1}}}{u}=\dfrac{{{\mu }_{2}}-{{\mu }_{2}}}{R}$ and find the position of the first image. This will act as an object for surface S’ and gain use of the same formula to find the position of the final image.

Formula used:
$\dfrac{{{\mu }_{2}}}{v}-\dfrac{{{\mu }_{1}}}{u}=\dfrac{{{\mu }_{2}}-{{\mu }_{2}}}{R}$

Complete step by step answer:
When rays of light from an object passes through a spherical mirror, the light refracts and an image is formed of the object. The relation between the positions of the object and its image is given as $\dfrac{{{\mu }_{2}}}{v}-\dfrac{{{\mu }_{1}}}{u}=\dfrac{{{\mu }_{2}}-{{\mu }_{2}}}{R}$ …. (1).
In this formula, ${{\mu }_{1}}$ is the refractive index of the medium in which the light is incident and ${{\mu }_{2}}$ is the refractive index of the medium in which the light enters after refraction. R is the radius of the spherical surface.
The values of v, u and R are according to the sign convection.
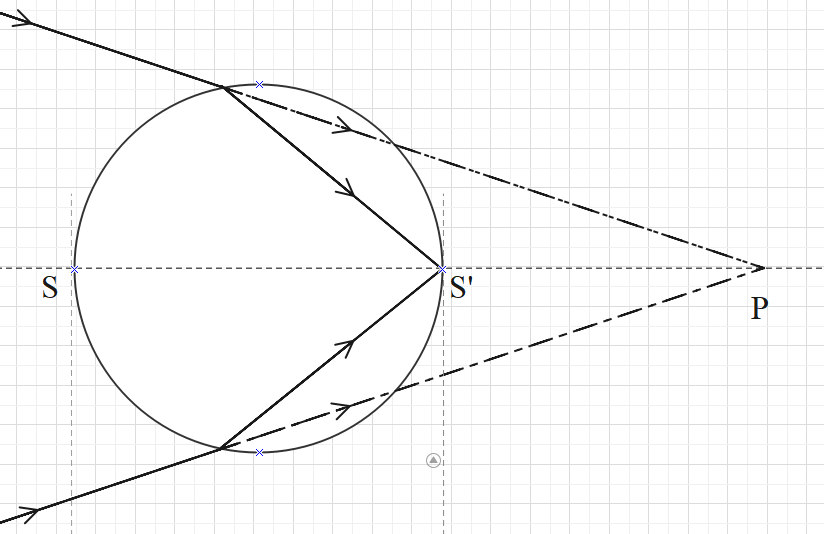
In the given case, the light will be refracted twice. First at surface S and next at surface S’.
Let apply formula 1 to the refraction at surface S. Here, the light is coming from infinity and converging at a point P. Point P acts as a virtual object. Hence, $u=20$. R = 5cm.
The light is entering from air into the glass sphere. Hence, ${{\mu }_{1}}=1$ and ${{\mu }_{2}}=1.5$.
And the position of the image be v’.
Substitute the values in equation (1).
$\Rightarrow \dfrac{1.5}{v'}-\dfrac{1}{20}=\dfrac{1.5-1}{5}$
$\Rightarrow \dfrac{1.5}{v'}=\dfrac{0.5}{5}+\dfrac{1}{20}$
$\Rightarrow \dfrac{1.5}{v'}=\dfrac{2+1}{20}=\dfrac{3}{20}$
$\Rightarrow v'=1.5\times \dfrac{20}{3}=10cm$
This means that the first image of the object is formed at a distance of 10cm towards the right of surface S.
Now, this image will act as an object for surface S’ and hence a final image is formed when the light comes out of the glass.
Let the position of the final image be v.
The first image is located at a distance of 10 cm towards the right of S and the distance between the surfaces S and S’ is 10 cm. Therefore, the position of the first image from surface S’ is 10-10=0cm.
This means that u = 0cm.
In this case, the light is entering from the glass sphere into the air. Hence, ${{\mu }_{1}}=1.5$ and ${{\mu }_{2}}=1$. And R= -5cm.
Substitute the values in equation (1).
$\Rightarrow \dfrac{1}{v}-\dfrac{1.5}{0}=\dfrac{1-1.5}{-5}$
$\Rightarrow \dfrac{1}{v}-\infty =\dfrac{-0.5}{-5}=\dfrac{0.1}{1}$
$\Rightarrow \dfrac{1}{v}=\dfrac{0.1}{1}+\infty$
When a finite number is added to infinity, the value of the sum remains infinity.
Hence,
$\dfrac{1}{v}=\infty$
This implies,
$v=\dfrac{1}{\infty }$
$\Rightarrow v=0$
This means that the final image is at a distance of 0cm from surface S’.
Therefore, when the light passes from the glass sphere into air, no refraction takes place.
Hence, the position of the image is at the right end of the horizontal diameter of the glass sphere, as shown in the diagram.

Note:
From this question we can make note that when all the rays of light pass through the pole of the spherical surface, the rays do not refract. Thus no image is formed. Here, the pole is the midpoint of the spherical surface.