Question

A copper rod of diameter 1 cm and length 8 cm is drawn into a wire of length 18 m of uniform thickness. Find the thickness of the wire.

Answer 1

Hint: It is said that a copper rod is converted into a wire. So the volume of the copper rod and wire will be the same. The volume of these is similar to that of a cylinder. Find the volume of copper rod and equate it to the volume of wire, to get the diameter of wire.



Complete step-by-step answer:
Consider the 2 figures drawn. Thus we can say that the volume of the copper rod will be equal to the volume of wire.

\[\therefore \]Volume of copper rod = Volume of wire.

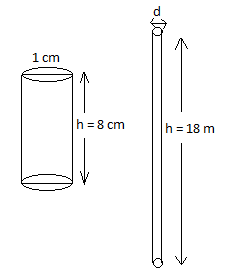
First let us find the volume of copper rod. The copper rod is in the form of a cylinder with a diameter of 1 cm. Let’s take the radius of the rod as ‘r’.
Diameter of rod = 1 cm.
Radius of rod \[=r=\dfrac{d}{2}=\dfrac{1cm}{2}=0.5cm.\]
The length of the rod is equal to the height ‘h’ of the rod.
\[\therefore \]Height of rod \[=h=8cm.\]
Thus we can find the volume of the rod, which is in the shape of a cylinder.
\[\therefore \]Volume of rod \[=\pi {{r}^{2}}h.\]
We know r = 0.5 cm and h = 8 cm. Substitute and get the volume of rod.
Volume of rod \[\begin{align}
  & =\pi \times {{(0.5)}^{2}}\times 8 \\
 & =\pi \times 0.5\times 0.5\times 8=2\pi c{{m}^{3}}. \\
\end{align}\]
Volume of rod \[=2\pi c{{m}^{3}}.\]
Now let us find the volume of wire.
The wire is in the form of a cylinder with radius ‘r’ and height ‘h’.
The length of wire is equal to the height of wire, h = 8 m.
\[\begin{align}
  & h=18m=18\times 100cn=1800cm. \\
 & \therefore 1m=100cm. \\
\end{align}\]
Volume of wire \[\begin{align}
  & =\pi {{r}^{2}}h \\
 & =\pi \times {{r}^{2}}\times 1800 \\
 & =1800\pi {{r}^{2}}c{{m}^{3}}. \\
\end{align}\]
Let us find that,
Volume of copper rod = Volume of wire
\[\begin{align}
  & 2\pi c{{m}^{3}}=1800\pi {{r}^{2}}c{{m}^{3}} \\
 & \Rightarrow 1800\pi {{r}^{2}}=2\pi . \\
\end{align}\]
Let us cancel out common terms and simplify it.
\[{{r}^{2}}=\dfrac{2}{1800}=\dfrac{1}{900}\Rightarrow \sqrt{{{r}^{2}}}=\sqrt{\dfrac{1}{900}}.\]
Taking square on both sides, we get,
\[r=\dfrac{1}{30}cm.\]
Hence the radius of the wire is \[\dfrac{1}{30}cm\].
Thickness of wire = Diameter of wire\[=2\times \]radius of wire\[=2\times \dfrac{1}{30}=\dfrac{1}{15}cm.\]
We got the thickness of the wire as \[\dfrac{1}{15}cm\].

Note:
Here the same quantity of the material is used to reshape the copper rod to wire. So we can say that their volume will be the same irrespective of their height and radius. We have used the volume of the cylinder as copper rod and wire similar to it.