Question

A copper wire, 3mm in diameter, is wound about a cylinder whose length is 12cm, and diameter 10 cm, so as to cover the curved surface of the cylinder. Find the length and mass of the wire, assuming the density of copper to be 8.88\[g/c{m^3}\].

Answer 1

Hint: In this question, first we will make the diagram indicating a turn of wire. Then we will calculate the total number of turns of wire required by dividing the height of the cylinder by the diameter of the wire. The length of the wire is equal to the multiplication of the total of turns and length for one turn. Finally, we will calculate the volume of the wire to get the mass of the wire.

Complete step-by-step solution:
The diagram is given below:

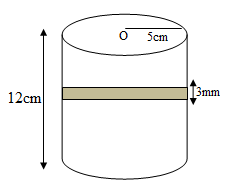
Height of cylinder = 12cm
Diameter of cylinder =10cm
Radius of cylinder= 5cm
Diameter of wire = 3mm = 0.3cm
From the diagram, we can say that 1 round of wire will cover 3mm of height.
So, the number of rounds= $\dfrac{{{\text{Height of cylinder}}}}{{{\text{Diameter of wire}}}} = \dfrac{{12cm}}{{0.3cm}}$= 40 rounds.
Total length of wire in one rotation = circumference of base of cylinder =$2\pi r = 2\pi \times 5 = 10\pi $cm
Total length of wire in 40 rounds =length in one rotation $ \times $total rotation
=$40 \times 10\pi = \dfrac{{400 \times 22}}{7}$ =1257.14cm = $\dfrac{{1257.14}}{{100}}$ =12.57m.
Now, radius of wire =$\dfrac{{Diameter}}{2} = \dfrac{{0.3}}{2}$ =0.15cm.
We know that volume = Area of cross section $ \times $ length.
So, putting the values in the above equation. we have:
Volume of wire =$\pi {r^2} \times length = \pi {\left( {0.15} \right)^2} \times 1257.14 = 88.898c{m^3}$.
Now, we know that mass = volume $ \times $density.
Therefore, mass of wire = 88.898$ \times $8.88 = 789.41gm.

Note: In this question the crucial step is a calculation of total round of wire. This is simply an application of a unitary method. So, you should have a good idea of unitary methods. The base of the cylinder is a circle, so we have used formula $2\pi r$to calculate the circumference which also gives the length of wire for one turn. Circumference of the circle is also given by the formula ‘$\pi d$’ where ‘d’ is the diameter.