Question

A couple formed by two equal and opposite forces of 8N & separated by distance 3m acts on a body in clockwise direction. This couple can be balanced by another couple having
A. F = 6N & r = 4m in clockwise direction
B. F = 4N & r = 6m in clockwise direction
C. F = 6N & r = 4m in anticlockwise direction
D. F = 4N & r = 3m in anticlockwise direction

Answer 1

Hint: We can solve this problem, easily, once we understand the concept of couples. They are parallel forces acting on either end in opposite directions. We can find the moment of a couple from the magnitude of the force and the distance between them. This couple can only be balanced by another couple which is equal in magnitude and opposite in direction.

Formula used:
$M = F \times d$

Complete step-by-step answer:
Couples are parallel forces that are equal in magnitude acting on either end, causing a pure rotational motion. If we draw a diagram for the given couples, it would look something like this.

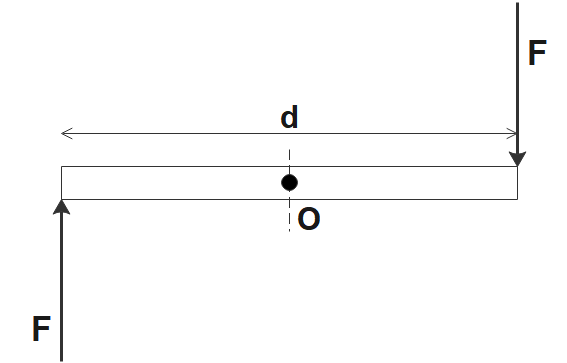
The moment due to a couple is given by
$M = F \times d$
Where,
M is the moment of the couple
F is the magnitude of the force
d is the perpendicular distance between the forces
In the question, they’ve given us a couple of forces, 8N acting at a distance of 3m. So, the moment due to this couple will be
$\eqalign{
  & M = F \times d \cr
  & \Rightarrow M = 8N \times 3m \cr
  & \Rightarrow M = 24Nm \cr} $
Now, the moment of the balancing couple must be equal to 24Nm but its direction must be anticlockwise, to counter the moment which is in the clockwise direction.
Therefore, this condition is only held by option C.
So, the correct answer is “Option C”.

Note: You must not confuse couples for torque. In contrast to couples, a torque acts in one direction or on one side while the other side is pivoted. Torque can produce translational motion, while couples only produce rotational motion and no translational motion. One can say that couples are a special case of torque where there is a center of rotation.