
A cube is painted red on all sides is cut into 125 equal small cubes. A small cube when picked up is found to show red colour on one side of its face. The probability that two more faces also show red colour is.
(a) $\dfrac{4}{49}$
(b) $\dfrac{1}{13}$
(c) $\dfrac{3}{49}$
(d) $\dfrac{4}{51}$
Answer
598.5k+ views
Hint: For solving this question as we have to find the probability of the given event for which first we have to find the number of favourable cases for that event and the total number of cases possible. For the total number of cases, we will find the number of cubes which have at least one face is painted and the number of favourable cases will be the number of cubes whose $1+2=3$ faces are painted. After that, we will solve each part for their correct answer.
Complete step-by-step solution -
Given:
It is given that a cube is painted red on all sides is cut into 125 equal small cubes and a small cube when picked up is found to show red colour on one side of its face and we have to find the probability that two more faces of the selected cube will show red colour.
Now, in this problem, we have to find the probability of the given event for which first we have to find the number of favourable cases for that event and the total number of cases possible. After calculating both we can find the probability as per the following relation:
$P(E)=\dfrac{F}{T}..................\left( 1 \right)$
Where,
$P(E)=$Probability of event E.
$F=$The number of favourable cases for the event E.
$T=$Total number of cases possible.
Now, here the total number of cases will be the number of cubes which have at least one face is painted and the number of favourable cases will be the number of cubes whose $1+2=3$ faces are painted.
Now, we can visualise the given situation with the help of the following figure:
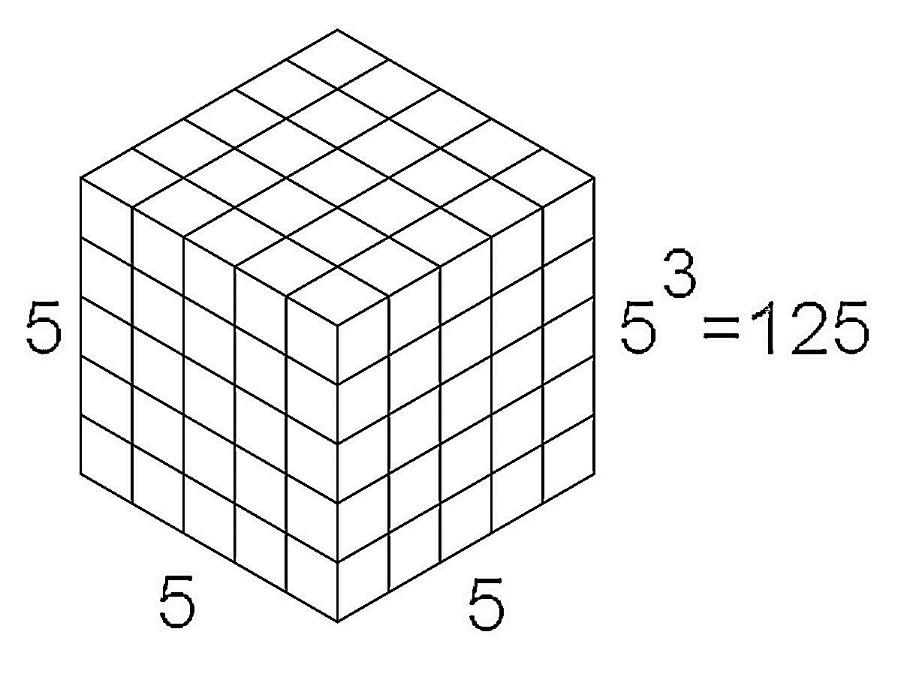
In the above figure, there is a cube of edge size 5 units and we can cut it into 125 cubes of equal sizes of edge 1 unit.
Now, when we paint it and cut it then we will get a total 125 number of cubes. And instead of calculating the number of cubes which have at least one face is painted, we should find the number of cubes which have no face painted as it is a much easier task.
Now, when we paint the bigger cube and cut it as per the given data then, we will find that after removing the first layer of cubes from every face, we will get the cubes which have no face painted. To visualise this, we can think that initially, we have a cube of edge 5 units and if we cut the first layer of cubes of edge 1 unit from each face then, we will get a cube of size $5-2=3$ units. Which means there will be ${{3}^{3}}=27$ such cubes which will have no face painted. And to get the number of cubes which have at least one face is painted, we should subtract the number of cubes which have no face painted from the total number of cubes. Then,
Total number of cases possible $=T=125-27=98.............\left( 2 \right)$
Now, we have to find the number of cubes which have 3 faces painted.
Now, if we see the diagram then we will find that smaller cubes which will have the vertex of the bigger cube will have its 3 faces painted and as the bigger cube has 8 vertices so, there will be 8 such cubes which have 3 faces painted. Then,
The number of favourable cases for the given event $=F=8...............\left( 3 \right)$
Now, substitute the value of $T=98$ from equation (2) and $F=8$ from equation (3) into equation (1). Then,
$\begin{align}
& P(E)=\dfrac{F}{T} \\
& \Rightarrow P(E)=\dfrac{8}{98} \\
\end{align}$
$\Rightarrow P(E)=\dfrac{4}{49}$
Now, from the above result, we conclude that probability for the given event will be $\dfrac{4}{49}$ .
Hence, (a) will be the correct option.
Note: Here, the student should first try to understand what is asked in the question. After that, we should apply the very basic concept of probability and directly apply the formula. Moreover, we can apply the direct formula ${{\left( n-2 \right)}^{3}}$ to find the number of cubes which have no face painted with the value of $n=5$ , and we should proceed stepwise and avoid calculation mistake while solving the question to get the correct answer.
Complete step-by-step solution -
Given:
It is given that a cube is painted red on all sides is cut into 125 equal small cubes and a small cube when picked up is found to show red colour on one side of its face and we have to find the probability that two more faces of the selected cube will show red colour.
Now, in this problem, we have to find the probability of the given event for which first we have to find the number of favourable cases for that event and the total number of cases possible. After calculating both we can find the probability as per the following relation:
$P(E)=\dfrac{F}{T}..................\left( 1 \right)$
Where,
$P(E)=$Probability of event E.
$F=$The number of favourable cases for the event E.
$T=$Total number of cases possible.
Now, here the total number of cases will be the number of cubes which have at least one face is painted and the number of favourable cases will be the number of cubes whose $1+2=3$ faces are painted.
Now, we can visualise the given situation with the help of the following figure:
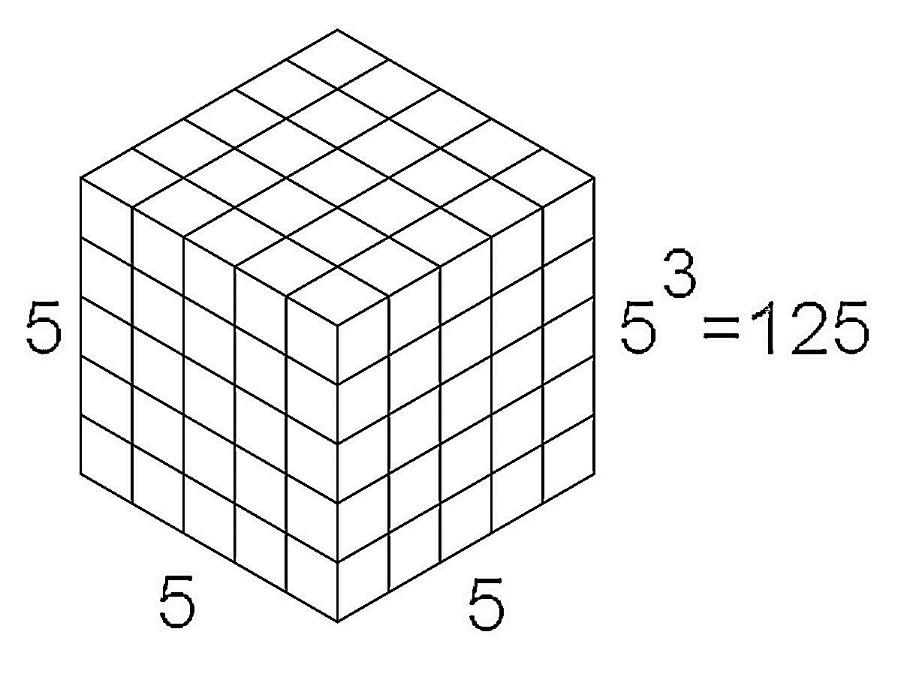
In the above figure, there is a cube of edge size 5 units and we can cut it into 125 cubes of equal sizes of edge 1 unit.
Now, when we paint it and cut it then we will get a total 125 number of cubes. And instead of calculating the number of cubes which have at least one face is painted, we should find the number of cubes which have no face painted as it is a much easier task.
Now, when we paint the bigger cube and cut it as per the given data then, we will find that after removing the first layer of cubes from every face, we will get the cubes which have no face painted. To visualise this, we can think that initially, we have a cube of edge 5 units and if we cut the first layer of cubes of edge 1 unit from each face then, we will get a cube of size $5-2=3$ units. Which means there will be ${{3}^{3}}=27$ such cubes which will have no face painted. And to get the number of cubes which have at least one face is painted, we should subtract the number of cubes which have no face painted from the total number of cubes. Then,
Total number of cases possible $=T=125-27=98.............\left( 2 \right)$
Now, we have to find the number of cubes which have 3 faces painted.
Now, if we see the diagram then we will find that smaller cubes which will have the vertex of the bigger cube will have its 3 faces painted and as the bigger cube has 8 vertices so, there will be 8 such cubes which have 3 faces painted. Then,
The number of favourable cases for the given event $=F=8...............\left( 3 \right)$
Now, substitute the value of $T=98$ from equation (2) and $F=8$ from equation (3) into equation (1). Then,
$\begin{align}
& P(E)=\dfrac{F}{T} \\
& \Rightarrow P(E)=\dfrac{8}{98} \\
\end{align}$
$\Rightarrow P(E)=\dfrac{4}{49}$
Now, from the above result, we conclude that probability for the given event will be $\dfrac{4}{49}$ .
Hence, (a) will be the correct option.
Note: Here, the student should first try to understand what is asked in the question. After that, we should apply the very basic concept of probability and directly apply the formula. Moreover, we can apply the direct formula ${{\left( n-2 \right)}^{3}}$ to find the number of cubes which have no face painted with the value of $n=5$ , and we should proceed stepwise and avoid calculation mistake while solving the question to get the correct answer.
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
The shortest day of the year in India

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




