Question

A cube with edges of length ‘b’ is divided into 8 smaller cubes. Calculate the difference between the combined surface area of the 8 smaller cubes and the surface area of the original cube.
$\begin{align}
  & \left( A \right)\dfrac{3}{2}{{b}^{2}} \\
 & \left( B \right)\dfrac{3}{4}{{b}^{2}} \\
 & \left( C \right)\dfrac{9}{2}{{b}^{2}} \\
 & \left( D \right)6{{b}^{2}} \\
 & \left( E \right)12{{b}^{2}} \\
\end{align}$

Answer 1

Hint: The larger cube has been divided into smaller cubes, so the volume of the cube is conserved. We will use this fact to calculate the edge length of smaller cubes. The volume of a cube is equal to the cube of its edge length. To calculate the difference in surface areas of the bigger cube and the smaller cubes, we will use the formula for surface area of the cube, which is equal to six times the edge squared.

Complete step by step answer:
We have been given a large cube whose edge length is ‘b’. This cube has been divided into 8 smaller cubes. Let the edge length of these smaller cubes be denoted by ‘x’.

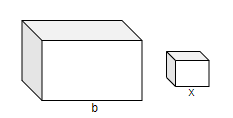
Then, applying the conservation of volume, we get:
$\begin{align}
  & \Rightarrow {{b}^{3}}=8\left( {{x}^{3}} \right) \\
 & \Rightarrow {{x}^{3}}=\dfrac{{{b}^{3}}}{8} \\
 & \therefore x=\dfrac{b}{2} \\
\end{align}$
Now that we have the edge length of the smaller cube, we can calculate its surface area along with the surface area of the original bigger cube.
Let the surface area of the bigger cube be denoted by ‘S’, then it is equal to:
$\Rightarrow S=6\left( {{b}^{2}} \right)$
Now, let the surface area of the 8 smaller cubes combined be denoted by ‘s’, then it is equal to:
$\begin{align}
  & \Rightarrow s=8\times \left[ 6{{\left( \dfrac{b}{2} \right)}^{2}} \right] \\
 & \Rightarrow s=8\times \left[ \dfrac{6{{b}^{2}}}{4} \right] \\
 & \Rightarrow s=12{{b}^{2}} \\
\end{align}$
Thus, the difference between the combined surface area of the 8 smaller cubes and the surface area of the original cube will be equal to:
$\begin{align}
  & \Rightarrow \left| S-s \right|=\left| 6{{b}^{2}}-12{{b}^{2}} \right| \\
 & \Rightarrow \left| S-s \right|=\left| -6{{b}^{2}} \right| \\
 & \therefore \left| S-s \right|=6{{b}^{2}} \\
\end{align}$
Hence, the difference between the combined surface area of the 8 smaller cubes and the surface area of the original cube comes out to be $6{{b}^{2}}$.
So, the correct answer is “Option D”.

Note: Here, we can clearly see that, even though the volume has remained constant, the total surface area has increased. In fact, greater the number of smaller cubes, greater the increase in surface area of the resulting fragments combined and lesser the number of smaller cubes, lesser the increase in surface area.