Question

A cubic box of 120cm has to be filled with cuboidal books of dimensions $20cm\times 12cm\times 6cm$. How many such books can be filled in the cubical box?

Answer 1

Hint: We here have been given a cuboid box with its dimensions and books which have all the dimensions along with their dimensions and we have been asked to find the number of books that can be fitted into this box. For this, we will first assume the number of books that can be fitted ‘n’. Then we will find the volume of the box and then the volume of each book. Then we will find the total volume of n books by multiplying the volume of each book by n. Then we will keep the volume of the box equal to the total volume of n books. Then we will solve for n from this equation and hence we will find our required answer.

Complete step-by-step solution
Here, the total volume of the maximum books that can be filled in the box is equal to the volume of the cubic box.
Let us first assume the number of books that can fit into the box to be ‘n’.
Now, we will first calculate the volume of the cubic box:
We know that the volume of the cubic box if side ‘a’ is given as, ${{a}^{3}}$.
Here, we have a=120cm

Thus, the volume of the cube is:
$\begin{align}
  & volume={{\left( 120 \right)}^{3}} \\
 & volume=1728000c{{m}^{3}} \\
\end{align}$
Now, we will calculate the volume of one book:
We know that the volume of a cuboid box with dimensions $l\times b\times h$ is given as $lbh$.
Here we have $l\times b\times h=20cm\times 12cm\times 6cm$

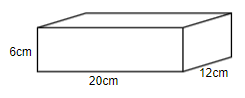
Thus, the volume of the book is:
$\begin{align}
  & volume=\left( 20cm \right)\left( 12cm \right)\left( 6cm \right) \\
 & volume=1440c{{m}^{3}} \\
\end{align}$
Now, the number of books that can be filled into the box is ‘n’.
Thus, the total volume of the books which can be filled into this box is:
$\begin{align}
  & n\times 1440 \\
 & \Rightarrow 1440nc{{m}^{3}} \\
\end{align}$
Now, as mentioned above, the maximum value of this total volume is equal to the volume of the box.
Thus, we can say that:
$1440n=1728000$
Now, solving this equation for ‘n’, we get:
$\begin{align}
  & 1440n=1728000 \\
 & \Rightarrow n=\dfrac{1728000}{1440} \\
 & \therefore n=1200 \\
\end{align}$
Thus, the number of books that can fit into the box is 1200.

Note: We should always take care of the units in these types of questions. Here, all the units are the same, i.e. ‘cm’ but there are many questions in which the units are different for different dimensions. In those cases, we should make all the units the same first and then compare them otherwise it will result in a wrong answer.