
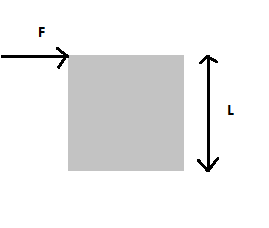
A cubical block of side L rests on a rough horizontal surface with the coefficient of friction $\mu $. A horizontal force F is applied on the block as shown in the figure. If the coefficient is sufficiently high so that the block does not slide before toppling, the minimum force required to topple the block is
A. Infinitesimal
B. $\dfrac{{mg}}{4}$
C. $\dfrac{{mg}}{2}$
D. $mg(1 - \mu )$

Answer
557.4k+ views
Hint: In this question, we need to determine the minimum force required to topple the block such that the cubical block of side L rests on a rough horizontal surface with the coefficient of friction $\mu $. As we can see that this is a case of toppling. For toppling we need to equate the different torques applied and then find the expression.
Complete step by step answer:
Given the mass of block and is the side length of the block
For toppling, the normal reaction of the block comes to the extreme corner of the block touching the ground. Any further shift of normal reaction will result in the toppling. This is the limiting condition
Now if any force passes through the point of rotation it won’t produce any torque.
Thus here the normal reaction and the frictional force don’t produce any torque.
Now the torque produced by weight is anticlockwise while the torque by the applied force will be clockwise.
Since we want the minimum condition, we equate both the torques and we get that
$
F \times l = mg \times \dfrac{L}{2} \\
\implies F = \dfrac{{mg}}{2} \\
$
So, the correct answer is “Option C”.
Note:
Remember that if the force passes through the point of rotation it won’t produce any torque. Torques should be balanced carefully. One should know the directions in which the torque is produced. Also remember that frictional force and normal reaction doesn’t produce any torque. So do not include them.
Complete step by step answer:
Given the mass of block and is the side length of the block
For toppling, the normal reaction of the block comes to the extreme corner of the block touching the ground. Any further shift of normal reaction will result in the toppling. This is the limiting condition
Now if any force passes through the point of rotation it won’t produce any torque.
Thus here the normal reaction and the frictional force don’t produce any torque.
Now the torque produced by weight is anticlockwise while the torque by the applied force will be clockwise.
Since we want the minimum condition, we equate both the torques and we get that
$
F \times l = mg \times \dfrac{L}{2} \\
\implies F = \dfrac{{mg}}{2} \\
$
So, the correct answer is “Option C”.
Note:
Remember that if the force passes through the point of rotation it won’t produce any torque. Torques should be balanced carefully. One should know the directions in which the torque is produced. Also remember that frictional force and normal reaction doesn’t produce any torque. So do not include them.
Recently Updated Pages
Why are manures considered better than fertilizers class 11 biology CBSE

Find the coordinates of the midpoint of the line segment class 11 maths CBSE

Distinguish between static friction limiting friction class 11 physics CBSE

The Chairman of the constituent Assembly was A Jawaharlal class 11 social science CBSE

The first National Commission on Labour NCL submitted class 11 social science CBSE

Number of all subshell of n + l 7 is A 4 B 5 C 6 D class 11 chemistry CBSE

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE




