Question

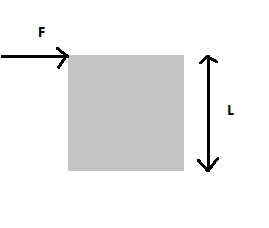
A cubical block of side L rests on a rough horizontal surface with the coefficient of friction $\mu $. A horizontal force F is applied on the block as shown in the figure. If the coefficient is sufficiently high so that the block does not slide before toppling, the minimum force required to topple the block is

A. Infinitesimal
B. $\dfrac{{mg}}{4}$
C. $\dfrac{{mg}}{2}$
D. $mg(1 - \mu )$

Answer 1

Hint: In this question, we need to determine the minimum force required to topple the block such that the cubical block of side L rests on a rough horizontal surface with the coefficient of friction $\mu $. As we can see that this is a case of toppling. For toppling we need to equate the different torques applied and then find the expression.

Complete step by step answer:
Given the mass of block and is the side length of the block
For toppling, the normal reaction of the block comes to the extreme corner of the block touching the ground. Any further shift of normal reaction will result in the toppling. This is the limiting condition
Now if any force passes through the point of rotation it won’t produce any torque.
Thus here the normal reaction and the frictional force don’t produce any torque.
Now the torque produced by weight is anticlockwise while the torque by the applied force will be clockwise.
Since we want the minimum condition, we equate both the torques and we get that
$
  F \times l = mg \times \dfrac{L}{2} \\
\implies F = \dfrac{{mg}}{2} \\
$

So, the correct answer is “Option C”.

Note:
Remember that if the force passes through the point of rotation it won’t produce any torque. Torques should be balanced carefully. One should know the directions in which the torque is produced. Also remember that frictional force and normal reaction doesn’t produce any torque. So do not include them.