Question

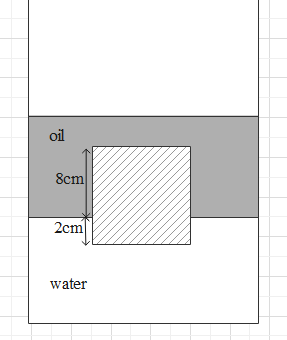
A cubical block of wood of side of 10 cm floats at the interface between oil and water as shown in figure with its lower face 2cm below the interface. The density of oil is $0.6gc{m}^{-3}$. The mass of the block is

A. 600g
B. 680g
C. 800g
D. 200g

Answer 1

Hint: Since the block is floating, the net force on the block is zero. Therefore, equate the sum of buoyant forces exerted on the block by oil and water to the gravitational force on the body. Use $F_B=\rho V_{s}g$ to find both the buoyant forces. $F_g=mg$.

Formula used:
$F_B=\rho V_{s}g$
$F_g=mg$

Complete step by step answer:
To solve this problem we need the concept of buoyancy.
When a body of mass m is submerged in a liquid, the liquid pushes the body upwards. This means that other than the gravitational force acting on the body, there is one more force exerted by the liquid. This force is called the force of buoyancy or buoyant force. The direction of this force is always upwards and opposite to the direction of the gravitational force.

The value of the buoyant force is given as $F_B=\rho V_{s}g$.
In this formula $\rho$ is the density of the liquid, $V_s$ is the volume of the body that is submerged in the liquid and g is acceleration due to gravity.
We know that gravitational force is $F_g=mg$.
In this case, both the liquids (water and oil) will exert upwards forces on the cubical block. And the gravity will exert a downward force.
Let the buoyant forces exerted by the oil and water be $F_{B,oil}$ and $F_{B,water}$ respectively.
The free diagram of the block will be:

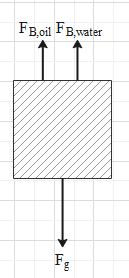
It is given that the block is floating. This means that the net force on the block is zero.
Therefore, the upward force balances the downward force.
Hence, $F_{B,oil}+F_{B,water}=F_g$ …. (i).
Let us calculate the value of $F_{B,oil}$.
Let the density of oil be ${\rho }_{oil}$. The volume of the body submerged in it is $V_{s,oil}$.
Therefore, $F_{B,oil}={\rho }_{oil}{V}_{s,oil}g$
It is given ${\rho }_{oil}=0.6gc{m}^{-3}$.
And $V_{s,oil}=10cm\times 10cm\times 8cm=800c{m}^3$.

Hence,
$F_{B,oil}=0.6\times 800g=480g$.
Let us calculate the value of $F_{B,water}$.
Let the density of oil be ${\rho }_{water}$. The volume of the body submerged in it is $V_{s,water}$.
Therefore, $F_{B,water}={\rho }_{water}{V}_{s,water}g$
${\rho }_{water}=1gc{m}^{-3}$.
And $V_{s,oil}=10cm\times 10cm\times 2cm=200c{m}^3$.
Hence,
$F_{B,oil}=1\times 200g=200g$.
And $F_g=mg$.

Substitute the values of $F_{B,water}$, $F_{B,oil}$ and $F_g$ in equation (i).
$\Rightarrow 480g+200g=mg$
$\Rightarrow 680g=mg$
$\Rightarrow m=680$
This means that the mass of the block is 680 grams.
Hence, the correct answer is option B.

Note:
Consider $F_B=\rho V_{s}g$ …… (1).
When a block is submerged in a liquid, it will displace a volume of liquid, which is equal to $V_s$.
Now, by using $mass=density\times volume$ the mass of the liquid displaced is $m_d=\rho V_s$.
Substitute the value of $\rho V_s$ in equation (1).
$\Rightarrow F_B=m_{d}g$
This means that the buoyant force is equal to the weight of the liquid displaced. Therefore, sometimes the buoyant force is referred to as the weight of the liquid displaced.