Question

A current carrying wire produces a magnetic field in its surrounding space. With the help of a diagram, derive an expression for the magnetic field at a point on the axis of circular loop current.

Answer 1

Hint: In this question we have been asked to find the magnetic field at a point on the axis of circular loop. We will be using the Biot – Savart law to solve this. The equation of Biot Savart law relates the magnetic field to the length, direction, magnitude and proximity of the current flowing through the loop. So, using this law we will calculate the current at point P lying on the axis of circular current loop.

Formula used:
\[dB=\dfrac{{{\mu }_{o}}Idl}{4\pi ({{R}^{2}}+{{x}^{2}})}\]
Where,
B is the magnetic field
I is the current in the loop
dl is the current element that produces the magnetic field at P
r is the distance between the current element dl and point P

Complete step-by-step answer:
                                     

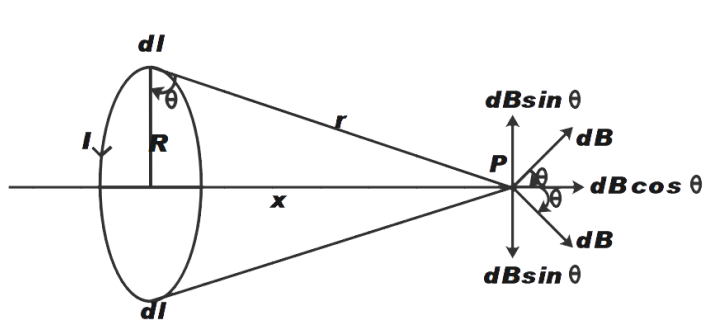
We have been asked to find the magnetic field at point P due to the current carrying element dl. So, assume any point P lying on the axis of circular current loop at a distance x and a small current carrying element dl on the circular loop as shown in the figure above.
Therefore, from Biot Savart equation,
\[dB=\dfrac{{{\mu }_{o}}Idl}{4\pi ({{R}^{2}}+{{x}^{2}})}\] ……….. (1)
We can calculate the magnetic field at P, where r is the distance between the point P and dl.
From Pythagoras theorem,
We know that,
\[{{r}^{2}}={{R}^{2}}+{{x}^{2}}\]
After substituting the value of r in equation (1)
We get,
\[dB=\dfrac{{{\mu }_{o}}Idl}{4\pi ({{R}^{2}}+{{x}^{2}})}\]
Now, from the figure it is clear that the vertical component of dB will be cancelled out since they are opposite in direction and have equal magnitude. Therefore, only the horizontal component of dB remains.
Therefore, we can say that the direction of the net magnetic field at point P is in the horizontal direction parallel to the axis of current in the loop.
Now to calculate the magnitude of magnetic field say \[{{B}_{p}}\] at point P
Therefore,
\[{{B}_{p}}=\int{dB\cos \theta }\] …………… (2)
From the figure we can say that
\[\cos \theta =\dfrac{R}{\sqrt{{{R}^{2}}+{{x}^{2}}}}\]
After substituting the above value in equation (2)
We get,
\[\therefore {{B}_{p}}=\dfrac{{{\mu }_{o}}IR}{4\pi {{({{R}^{2}}+{{x}^{2}})}^{{}^{3}/{}_{2}}}}\int{dl}\]
After integrating dl for complete circumference of the circular loop
We get,
\[{{B}_{p}}=\dfrac{{{\mu }_{o}}IR}{4\pi {{({{R}^{2}}+{{x}^{2}})}^{{}^{3}/{}_{2}}}}\times 2\pi R\]
Therefore,
\[{{B}_{p}}=\dfrac{{{\mu }_{o}}I{{R}^{2}}}{2{{({{R}^{2}}+{{x}^{2}})}^{{}^{3}/{}_{2}}}}\]
Therefore, the magnetic field at point P due to the circular current loop is \[{{B}_{p}}=\dfrac{{{\mu }_{o}}I{{R}^{2}}}{2{{({{R}^{2}}+{{x}^{2}})}^{{}^{3}/{}_{2}}}}\].

Note: French physicist Jean Baptiste Biot and Felix Savart, through their observations and calculations derived a mathematical expression. This equation states that the density of magnetic flux is directly proportional to the length of the current carrying element dl, the current I. It is also inversely proportional to the square of the distance between the current element and the given point.
This equation can be written as,
\[dB\propto \dfrac{Idl}{{{r}^{2}}}\]