
A cyclist moving on a circular track of radius
A. Zero.
B.
C.
D.
Answer
480.6k+ views
Hint:The displacement of the cyclist after covering the revolution is twice the radius of the circular track. Use the formula for average velocity of the body to determine the average velocity of the cyclist.
Formula used:
The average velocity of the body is,
Here,
Complete step by step answer:
We assume the initial position of the cyclist on the circular track is
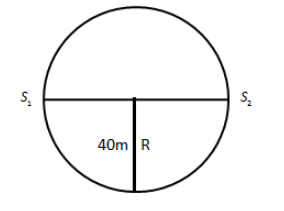
We have the formula for average velocity,
In the above figure, the displacement of the cyclist is,
Here, t is the time taken by the cyclist to complete a semicircle.
Substituting 40 m for R and 40 sec for t in the above equation, we get,
Therefore, the average velocity of the cyclist is 2 m/s.So, the correct answer is option C.
Note: Displacement of the body is the difference between its final and initial position. Therefore, the displacement in this case is twice the radius. Now the term distance covered by the cyclist means the circumference of half circle. Therefore, the distance covered by the cyclist is
Formula used:
The average velocity of the body is,
Here,
Complete step by step answer:
We assume the initial position of the cyclist on the circular track is

We have the formula for average velocity,
In the above figure, the displacement of the cyclist is,
Here, t is the time taken by the cyclist to complete a semicircle.
Substituting 40 m for R and 40 sec for t in the above equation, we get,
Therefore, the average velocity of the cyclist is 2 m/s.So, the correct answer is option C.
Note: Displacement of the body is the difference between its final and initial position. Therefore, the displacement in this case is twice the radius. Now the term distance covered by the cyclist means the circumference of half circle. Therefore, the distance covered by the cyclist is
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




