Question

A cylinder of mass M and radius R starts falling under gravity at t=0 as shown in the figure. If the mass of the chord is negligible, the tension in each string is?

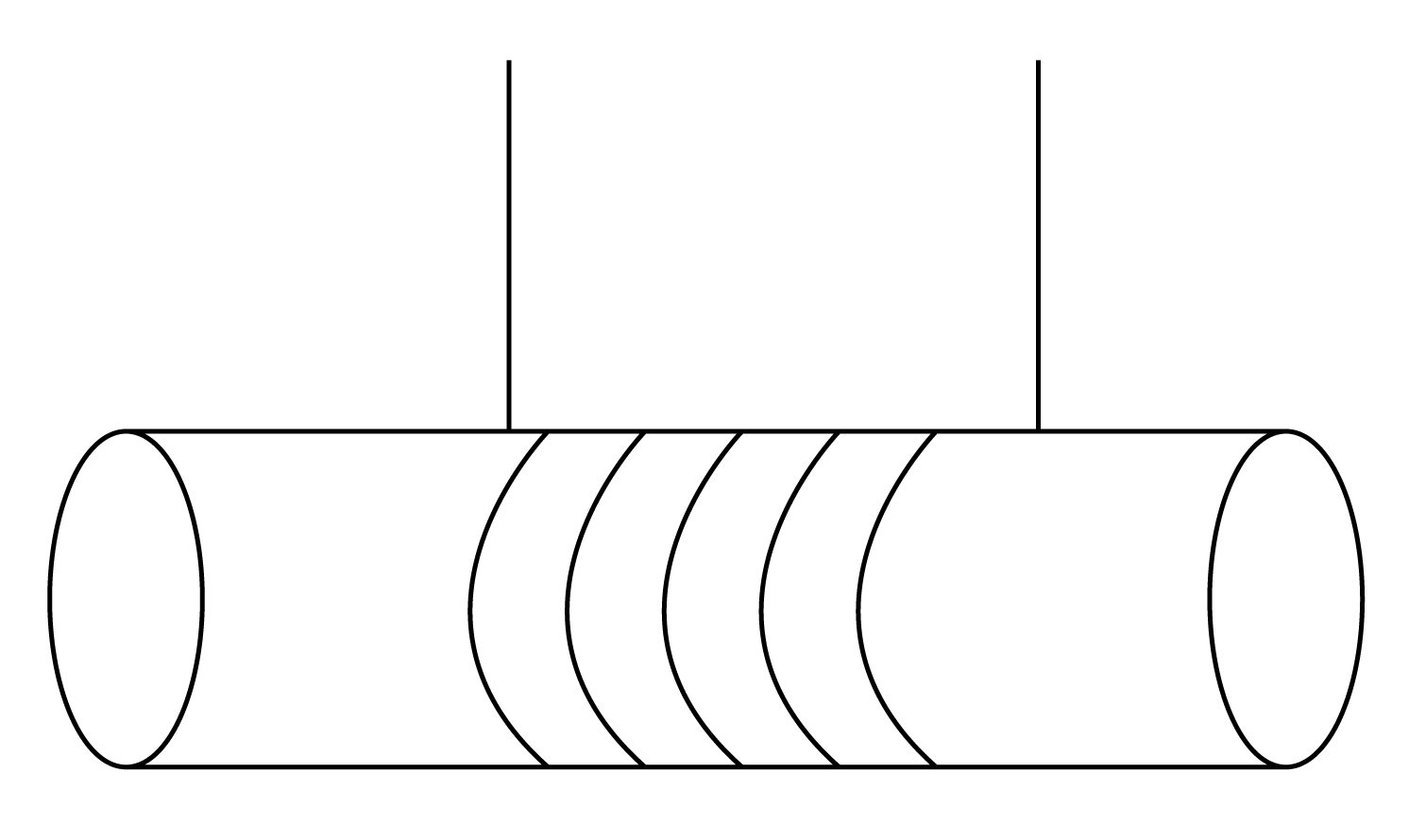
Answer 1

Hint: Hint: Pure rolling is the condition when there is no slipping at the surface at which the object is rolling. Under pure rolling the rotational kinetic energy is zero and only the linear velocity of the object exists.

 Complete step by step answer:
The Moment of inertia of the cylinder is given by:
\[I = \dfrac{{M{R^2}}}{2}\]
Here,I is the moment of inertia, R is the radius of the cylinder and M is the mass of the cylinder.
The equation of translation can be written as,
$Mg - 2T = Ma$ …… (A)
Here, T is the tension in the string and ‘a’ is the acceleration.
The equation of rotation can be written as,
$2TR = I\alpha $ ……. (I)
Here $\alpha $ is the angular acceleration.
Substitute \[I = \dfrac{{M{R^2}}}{2}\] in equation (I) and the equation becomes,
$2TR = \dfrac{{M{R^2}}}{2}\alpha $ ……. (II)
As the cylinder is rolling without slipping, hence the acceleration is,
$a = R\alpha $ ……. (III)
Combining equations (A), (II) and (III), it comes out to be,
$\begin{array}{c}
Mg - 2T = 4T\\
Mg = 6T\\
T = \dfrac{{Mg}}{6}
\end{array}$
Therefore, the tension in each string is $\dfrac{{Mg}}{6}$.

Note:
 The above question can also be solved by using D-Alembert’s principle which states that the summation of force and negative times the mass and acceleration of the moving body is equal to zero and the inertial force is taken into consideration.