Question

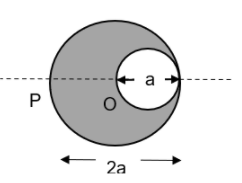
A cylindrical cavity of diameter ‘a’ exists inside a cylinder of diameter ‘2a’ as shown in the given figure. Both the cylinder and the cavity are infinitely long. A long uniform current density J flows along the length. The magnitude of the magnetic field at the point P is given by \[\dfrac{N}{12}{{\mu }_{0}}J\].Then the value of N is?

A.5
B.6
C.7
D.8

Answer 1

Hint: The magnetic field due to infinitely long cylinders can be used for both the cavity and the cylindrical cable. The resultant magnetic field due to these structures will be given an equation with the known variables from which the unknown can be derived.

Complete answer:
Let us consider an infinitely long cylindrical cable as the one given in the question.
According to Biot-Savart law, a current carrying element influences any point with a magnetics field. The strength and orientation is mainly dependent on the magnitude of the current and distance from the element to the point. It is given by –
\[B(r)=\dfrac{{{\mu }_{o}}}{4\pi }\int\limits_{c}{\dfrac{Idl\times \overrightarrow{r}}{{{r}^{3}}}}\]
From this we can derive the magnetic field at a point P, which is on the surface of the infinitely long cylindrical cable.
The magnetic field at point P due to cavity is given by -
\[{{B}_{1}}=\dfrac{{{\mu }_{0}}Ja}{2}\]
The magnetic field at point P due to the cylinder is given by –
 \[\begin{align}
  & {{B}_{2}}=\dfrac{{{\mu }_{0}}J{{\left( \dfrac{a}{2} \right)}^{2}}}{2\times \dfrac{3a}{2}} \\
 & {{B}_{2}}=\dfrac{{{\mu }_{0}}Ja}{12} \\
\end{align}\]
The total magnetic field is –
\[\begin{align}
  & B={{B}_{1}}+{{B}_{2}} \\
 & B=\dfrac{{{\mu }_{0}}Ja}{2}+\dfrac{{{\mu }_{0}}Ja}{12} \\
 & B=\dfrac{5{{\mu }_{0}}Ja}{12} \\
 & \Rightarrow N=5 \\
\end{align}\]
The unknown is 5.

The correct option is A.

Additional Information:
Ampere’s circuital law gives the magnetic field due to a point, whereas the Biot-Savart law gives the magnetic field at a point.

Note:
The derivation of the magnetic field at a point due to a cylinder from Biot-Savart involves considering the current element as a circle. On integrating to infinity we will find the appropriate equation for the magnetic at a point which is away, on or inside the cylinder.