Question

A cylindrical pillar is 50cm in diameter and 3.5m in height, find the cost of painting the curved surface of the pillar t the rate of Rs 12.50 per ${{\mathop{\rm m}\nolimits} ^2}$.

Answer 1

Hint:- The approach for solving this problem is – we have to first find the curved surface area of the pillar in ${{\mathop{\rm m}\nolimits} ^2}$and then for the total cost we have to multiply the total surface area with painting rate which is given in the question are per unitary method.

Complete step by step solution:

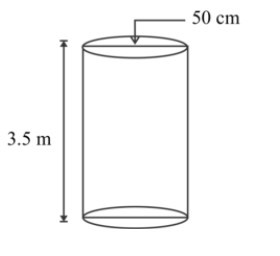
Given data,
Diameter = 50cm
Radius = 25cm
     =0.25m
Height of the pillar
     H = 3.5m
At first, we have to find the curved surface of the pillar.
We know that the curved surface area of a cylinder $2\pi {\mathop{\rm rh}\nolimits} {\left( {unit} \right)^2}$
$\therefore \;2\pi rh = 2 \times \dfrac{{22}}{7} \times 0.25 \times 3.5{{\mathop{\rm m}\nolimits} ^2}$
$\therefore $ Now are per question, the painting is applied only on the curved surface area, so we have to multiply painting cost by curved surface area,
$\therefore $painting cost = Rs 12.5 per ${{\mathop{\rm m}\nolimits} ^2}$
The total cost $ = 2 \times \dfrac{{22}}{7} \times 0.25 \times 3.5 \times 12.5$
     $ = 68.75$
So, the total painting cost is Rs 68.75.

Note: We have to very careful about where the painting is applied, because if paint is applied on both the upper surface and lower surface then we have to find the total surface area for that care by this formula $\left( {2\pi rh + 2\pi {r^2}} \right)$. Where $r = $ radius of base and $h = $height of the cylinder.