Question

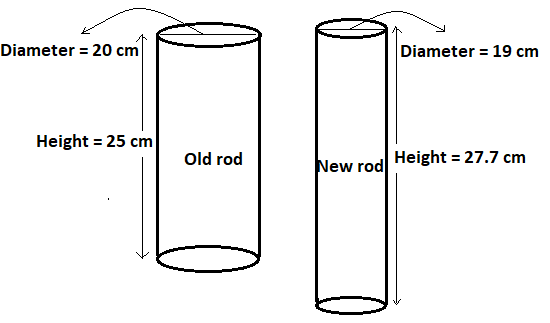
A cylindrical rod which is 25 cm long and of 20 cm in diameter is melted to form another rod of 19 cm diameter. Find the length of the new rod.

Answer 1

Hint: We had to only find the volume of both the cylindrical rod using formula V = \[\pi {r^2}h\] and then compare that to get the required length of the new rod.

Complete step-by-step solution -

As we know that if any shape is melted and then formed into another shape then the volume of both the shapes must be equal.
But here the cylindrical rod is melted and formed into a new cylindrical rod with different dimensions.
So, we had to compare their volumes to get the required length of the new cylindrical rod.
As we know that the volume of the cylinder is \[\pi {r^2}h\], where r is the radius of the cylinder and h is the length of the cylinder.
As given in the question, the diameter of the rod which is melted is 20 cm. So, its radius must be equal to \[\dfrac{{20}}{2} = 10\]cm
And the radius of new rod will be \[\dfrac{{19}}{2}\]cm
So, the volume of the cylindrical rod which is melted will be \[\pi {\left( {10} \right)^2}25 = 2500\pi {\text{ }}c{m^2}\]
Let the length of the new rod be h cm.
Now the volume of new rod will be equal to \[\pi {\left( {\dfrac{{19}}{2}} \right)^2}h = \dfrac{{361}}{4}\pi h{\text{ }}c{m^2}\]
So, \[2500\pi = \dfrac{{361}}{4}\pi h\]
Now cross multiplying the above equation and dividing both sides by \[\pi \]. We get,
10000 = 361h
Dividing both sides of the equation by 361. We get,
h = 27.7 cm.
Hence, the length of the new rod will be equal to 27.7 cm.

Note: Whenever we come up with this type of question then the volume of both the shapes (shape before melting and shape after melting) remains the same. So, to find the value of any unknown dimension I must assume that dimension and then we find the volume of both the shapes by applying formula to find the volume of that shape and then we compare both the volumes. And after solving that equation we will get the required unknown dimension (here length of the new rod).