
A. Derive an expression for the fringe width of the interference pattern formed on the screen.
B. Write the condition to produce a good interference band.
Answer
494.4k+ views
Hint: In this question, we need to start with the diagram of Young’s double-slit experiment. Then by using the coordinate geometry and approximation we get the path difference as $\vartriangle x = d\dfrac{y}{D}$ but we already know the equation of the path difference as \[\vartriangle x = n\lambda \] to get a bright fringe and $\Delta x = \left( {n + \dfrac{1}{2}} \right) \times \lambda $ to get a dark fringe pattern. So now equating these equations we get we will get the position of dark and bright fringe, then we subtract the bright fringe from the dark fringe for the same value of n, and we get $width = \dfrac{{D\lambda }}{d}$
Complete Step-by-Step solution:
First, we draw the diagram of interference using the double-slit experiment as shown in figure 1.
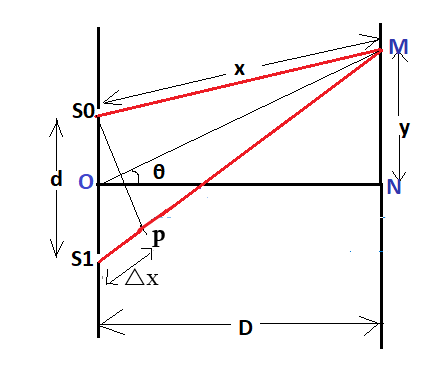
Here \[{S_1}\] and \[{S_0}\] are the slits which are $d$ distance apart.
$D$ is the distance between the screen and the slit.
Also $D \gg d$
Now we know the expression for the path difference is
\[\vartriangle x = n\lambda \] To get bright fringe ------------------ (1)
And $\Delta x = \left( {n + \dfrac{1}{2}} \right) \times \lambda $ to get a dark fringe---------- (2)
Now we assume that \[{S_1}M\] and \[{S_0}M\] are approximately parallel and hence \[{S_0}P\] is approximately perpendicular to \[{S_1}M\],\[{S_0}M\], and \[OM\].
Also as \[{S_0}P \bot OM\] and \[{S_1}{S_0} \bot ON\] therefore
\[\angle {S_0}{S_1}P = \angle MON = \theta \]
Now we can write the path difference as
$\vartriangle x = {S_1}M - {S_0}M \approx {S_1}M - PM$
$ \Rightarrow \vartriangle x = {S_1}P = d\sin \theta \approx d\tan \theta $
$ \Rightarrow \vartriangle x = d\dfrac{y}{D}$------------------------ (3)
We can see from the diagram that at a distance y from the center of the screen the center of the bright fringe is obtained. Now equating equation (1) and (3) we get
$ \Rightarrow \vartriangle x = n\lambda = d\dfrac{y}{D}$
$ \Rightarrow y = n\dfrac{{D\lambda }}{d}$
By putting $n = 1,2,3....$ we will get different positions of bright fringe that is
$ \Rightarrow y = 0, \pm 1\dfrac{{D\lambda }}{d}, \pm 2\dfrac{{D\lambda }}{d}, \pm 3\dfrac{{D\lambda }}{d}...$
And similarly, for dark fringe we will get
$ \Rightarrow y = \left( {n + \dfrac{1}{2}} \right)\dfrac{{D\lambda }}{d} = \pm 1\dfrac{{D\lambda }}{d}, \pm 3\dfrac{{D\lambda }}{d}, \pm 5\dfrac{{D\lambda }}{d}...$
Now to calculate the width we subtract the bright fringe from the dark fringe for the same value of n, and we get
$width = \dfrac{{D\lambda }}{d}$
B. It can be seen from the above equation that as the distance between the two slits is increasing and that d is increasing, the fringe width is reducing. If d becomes much higher than x, the fringe width will become quite small. Then the maxima and minima will become such closely spaced that it seems like a uniform intensity pattern on the screen. This result is an outcome of a simple theory that the effect of a wave is hard to observe if the wavelength is small in comparison to the dimensions of the obstacles or slits in the path of the incident wavefront.
Note: For these types of questions, we first need to remember Young’s double-slit experiment and the equations for path difference and positions of occurrence of the bright and dark fringes. After that, we need to have a clear understanding of how the interference gets affected when the distance between the two slits is increased or distance between the screen and the slits increases.
Complete Step-by-Step solution:
First, we draw the diagram of interference using the double-slit experiment as shown in figure 1.

Figure 1
Here \[{S_1}\] and \[{S_0}\] are the slits which are $d$ distance apart.
$D$ is the distance between the screen and the slit.
Also $D \gg d$
Now we know the expression for the path difference is
\[\vartriangle x = n\lambda \] To get bright fringe ------------------ (1)
And $\Delta x = \left( {n + \dfrac{1}{2}} \right) \times \lambda $ to get a dark fringe---------- (2)
Now we assume that \[{S_1}M\] and \[{S_0}M\] are approximately parallel and hence \[{S_0}P\] is approximately perpendicular to \[{S_1}M\],\[{S_0}M\], and \[OM\].
Also as \[{S_0}P \bot OM\] and \[{S_1}{S_0} \bot ON\] therefore
\[\angle {S_0}{S_1}P = \angle MON = \theta \]
Now we can write the path difference as
$\vartriangle x = {S_1}M - {S_0}M \approx {S_1}M - PM$
$ \Rightarrow \vartriangle x = {S_1}P = d\sin \theta \approx d\tan \theta $
$ \Rightarrow \vartriangle x = d\dfrac{y}{D}$------------------------ (3)
We can see from the diagram that at a distance y from the center of the screen the center of the bright fringe is obtained. Now equating equation (1) and (3) we get
$ \Rightarrow \vartriangle x = n\lambda = d\dfrac{y}{D}$
$ \Rightarrow y = n\dfrac{{D\lambda }}{d}$
By putting $n = 1,2,3....$ we will get different positions of bright fringe that is
$ \Rightarrow y = 0, \pm 1\dfrac{{D\lambda }}{d}, \pm 2\dfrac{{D\lambda }}{d}, \pm 3\dfrac{{D\lambda }}{d}...$
And similarly, for dark fringe we will get
$ \Rightarrow y = \left( {n + \dfrac{1}{2}} \right)\dfrac{{D\lambda }}{d} = \pm 1\dfrac{{D\lambda }}{d}, \pm 3\dfrac{{D\lambda }}{d}, \pm 5\dfrac{{D\lambda }}{d}...$
Now to calculate the width we subtract the bright fringe from the dark fringe for the same value of n, and we get
$width = \dfrac{{D\lambda }}{d}$
B. It can be seen from the above equation that as the distance between the two slits is increasing and that d is increasing, the fringe width is reducing. If d becomes much higher than x, the fringe width will become quite small. Then the maxima and minima will become such closely spaced that it seems like a uniform intensity pattern on the screen. This result is an outcome of a simple theory that the effect of a wave is hard to observe if the wavelength is small in comparison to the dimensions of the obstacles or slits in the path of the incident wavefront.
Note: For these types of questions, we first need to remember Young’s double-slit experiment and the equations for path difference and positions of occurrence of the bright and dark fringes. After that, we need to have a clear understanding of how the interference gets affected when the distance between the two slits is increased or distance between the screen and the slits increases.
Recently Updated Pages
Questions & Answers - Ask your doubts

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Science: Engaging Questions & Answers for Success

Full Form of IASDMIPSIFSIRSPOLICE class 7 social science CBSE

In case of conflict between fundamental rights of citizens class 7 social science CBSE

What percentage of the area in India is covered by class 10 social science CBSE

Trending doubts
The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Why is there a time difference of about 5 hours between class 10 social science CBSE

Who was Subhash Chandra Bose Why was he called Net class 10 english CBSE

Change the following sentences into negative and interrogative class 10 english CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

Explain the Treaty of Vienna of 1815 class 10 social science CBSE




