
A dip needle initially in the magnetic meridian when it shows an angle of dip
A.
B.
C.
D.
Answer
489.3k+ views
Hint: The angle of dip or simply dip is an angle made by the total magnetic field of the Earth, with its surface (or horizontal). The dip needle is the device used for measuring dip at a certain place. The change in the dip needle alters the horizontal component, as the dip circle is placed on a horizontal surface.
Formula used:
Complete answer:
The dip needle or dip circle is a device used to measure the dip angle at a given place. It is perfectly balanced about the horizontal axis. So that the needle is free to swing along the magnetic meridian.
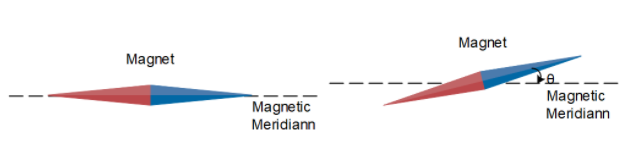
The dip angle is said to be the angle between the earth’s magnetic field and the horizontal. It varies from place to place. Mathematically it is given by,
Where,
According to the condition given in the question, let us say that initially the dip angle is
Once the dip circle is rotated through an angle
From the above equations, we can write
Therefore, the correct option is A.
Note:
Don’t be confused - Magnetic dip, dip, and magnetic inclination are interchangeably used for dip angle. Dip angles play a prominent role in the field of aviation. The lines plotted along the places where the dip angle or magnetic dip is the same are known as isoclinic lines. The line drawn joining the points where the dip angle is zero is called the magnetic equator.
Please observe that the magnetic meridian and geographic meridian of earth are completely different. The angle between the magnetic meridian and the geographic median is called the magnetic declination.
Formula used:
Complete answer:
The dip needle or dip circle is a device used to measure the dip angle at a given place. It is perfectly balanced about the horizontal axis. So that the needle is free to swing along the magnetic meridian.

The dip angle is said to be the angle between the earth’s magnetic field and the horizontal. It varies from place to place. Mathematically it is given by,
Where,
According to the condition given in the question, let us say that initially the dip angle is
Once the dip circle is rotated through an angle
From the above equations, we can write
Therefore, the correct option is A.
Note:
Don’t be confused - Magnetic dip, dip, and magnetic inclination are interchangeably used for dip angle. Dip angles play a prominent role in the field of aviation. The lines plotted along the places where the dip angle or magnetic dip is the same are known as isoclinic lines. The line drawn joining the points where the dip angle is zero is called the magnetic equator.
Please observe that the magnetic meridian and geographic meridian of earth are completely different. The angle between the magnetic meridian and the geographic median is called the magnetic declination.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE




