Question

A disc of mass m and radius r is free to rotate about its centre as shown in the figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system from rest. The speed of the block as it descends through a height h, is?

Answer 1

Hint: Use the concept of work energy theorem. According to the work energy theorem, the total work done on the system is equal to the change in the kinetic energy of the system. Find the work done on the system and the kinetic energy of the disc and the block.

Formula used:
$W=mgh$, work done by gravitational force when the block of mass m comes down by height h and g is acceleration due to gravity.
 $v=\omega R$, v is the speed of the rim of a disc rotating about its centre with radius R and angular velocity $\omega $.
${{K}_{1}}=\dfrac{1}{2}m{{v}^{2}}$, kinetic energy of a moving body.
${{K}_{2}}=\dfrac{1}{2}I{{\omega }^{2}}$, kinetic energy of a rotating body with moment of inertia I about its axis of rotation.

Complete step by step answer:
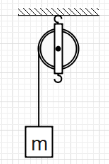
Let us assume that there is some friction between the string and the rim of the disc. As the block comes down under the influence of the gravitational force, the string will accelerate along the block and since there is friction between the string and the disc, the disc will rotate about the fixed point (i.e. its centre).

As the block comes down, the force of gravity will perform some work on the system of the block. The work done the gravitational force is equal to $W=mgh$.From the work energy theorem we know that the work done on a system is equal to the change in the kinetic energy of the system.

In this case, the kinetic energy of the system is equal to the sum of the kinetic energies of the block and the disc.Let the speed of the block when it comes down by a height of h be v. At this time, the speed of the string is also v. Since the string and the rim are moving along, the speed of the rim is equal to v.
But we know that $v=\omega R$.
$\Rightarrow \omega =\dfrac{v}{R}$ ….. (i)
The kinetic energy of the block at this time is ${{K}_{1}}=\dfrac{1}{2}m{{v}^{2}}$
And the kinetic energy of the disc is ${{K}_{2}}=\dfrac{1}{2}I{{\omega }^{2}}$
Since the system was released from rest, the change in kinetic energy of the system is $K=\dfrac{1}{2}m{{v}^{2}}+\dfrac{1}{2}I{{\omega }^{2}}$

Now substitute $\dfrac{1}{2}I{{\omega }^{2}}$ and $I=\dfrac{1}{2}m{{R}^{2}}$
$\Rightarrow K=\dfrac{1}{2}m{{v}^{2}}+\dfrac{1}{2}\left( \dfrac{1}{2}m{{R}^{2}} \right){{\left( \dfrac{v}{R} \right)}^{2}}$
$\Rightarrow K=\dfrac{1}{2}m{{v}^{2}}+\dfrac{1}{4}m{{v}^{2}}=\dfrac{3}{4}m{{v}^{2}}$
Now, equate W and K.
Then,
$\Rightarrow mgh=\dfrac{3}{4}m{{v}^{2}}$
$\Rightarrow {{v}^{2}}=\dfrac{4}{3}gh$
$\therefore v=\sqrt{\dfrac{4}{3}gh}$

Therefore, the speed of the block when it comes down by height of h is equal to $\sqrt{\dfrac{4}{3}gh}$.

Note:If we had not assumed the presence of the frictional force between the rim and the string, the block would come down under the gravitational force only with an acceleration of g. The work done by the frictional or the tension force in the string is zero because they are the internal force of the system and work done by the internal force of a system is always zero.