
A farmer connects a pipe of internal diameter
Answer
471k+ views
Hint: In this question we need to determine the time in which the tank will be filled. Here, we will determine the volume of pipe and the volume of the tank by using the volume of the cylinder formula, as both are in the shape of a cylinder. Then equate the volume of the pipe and volume of the tank to determine the height of the pipe. Then we will determine the time in which the tank will be filled when the rate of flow of water through the pipe is
Complete step-by-step answer:
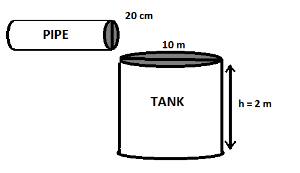
First, let us determine the volume of pipe and the volume of the tank separately.
Now, let us determine the volume of pipe,
Pipe is in the form of a cylinder.
Therefore, we know that the volume of cylinder
Here, it is given that the diameter of the pipe is
Now, we know that, radius
Therefore,
By converting
Let the length of the pipe for filling the whole tank be
Now, substituting the values in the volume of cylinder, we have,
Now, let us determine the volume of tank
Here, the tank is also in the form of a cylinder.
Therefore, we know that the volume of cylinder
It is given that the cylindrical tank is
Now, we know that, radius
It is also given that the cylindrical tank is
Therefore,
Substituting the values in the volume of a cylinder, we have,
Now, volume of pipe=volume of tank
Therefore,
It is given that water flows through the pipe at the rate of
We need to determine the time in which the tank will be filled.
Water flows in the pipe at the rate of
So, water flows in the pipe at the rate of
Therefore, water flows in the pipe at the rate of
We know that
Hence in
So, the correct answer is “
Note: In this question, it is important to note here that we can also solve this question by determining the volume of water that flows in
Complete step-by-step answer:

First, let us determine the volume of pipe and the volume of the tank separately.
Now, let us determine the volume of pipe,
Pipe is in the form of a cylinder.
Therefore, we know that the volume of cylinder
Here, it is given that the diameter of the pipe is
Now, we know that, radius
Therefore,
By converting
Let the length of the pipe for filling the whole tank be
Now, substituting the values in the volume of cylinder, we have,
Now, let us determine the volume of tank
Here, the tank is also in the form of a cylinder.
Therefore, we know that the volume of cylinder
It is given that the cylindrical tank is
Now, we know that, radius
It is also given that the cylindrical tank is
Therefore,
Substituting the values in the volume of a cylinder, we have,
Now, volume of pipe=volume of tank
Therefore,
It is given that water flows through the pipe at the rate of
We need to determine the time in which the tank will be filled.
Water flows in the pipe at the rate of
So, water flows in the pipe at the rate of
Therefore, water flows in the pipe at the rate of
We know that
Hence in
So, the correct answer is “
Note: In this question, it is important to note here that we can also solve this question by determining the volume of water that flows in
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
What was the capital of the king Kharavela of Kalinga class 9 social science CBSE

How many miles from the surface of Earth does space class 9 physics CBSE

Write an essay in about 150 200 words on the following class 9 english CBSE

21st March is celebrated as A World environment day class 9 biology CBSE

Explain the importance of pH in everyday life class 9 chemistry CBSE

Write the 6 fundamental rights of India and explain in detail




