
A field is in the shape of a trapezium whose parallel sides are 25m and 10m. If its non-parallel sides are 14m and 13m, find its area.
Answer
525.6k+ views
- Hint: In this question, we first need to draw the diagram with the given conditions. Then by using the formula for area of trapezium on substituting the respective values we can get the result.
Complete step-by-step solution -
TRAPEZIUM:
If one pair of opposite sides of a quadrilateral are parallel, then it is called a trapezium.
Area of a trapezium when the length of the parallel sides and non-parallel sides are given is
Where,
a, b are the parallel sides
c, d are the non-parallel sides
Let us now draw the diagram of the trapezium.
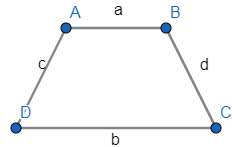
Given, in the question that
Now, from the above formula k is given by
Now, by substituting the respective values of a and b we get,
Let us now find the value of s from the above formula
Now, by substituting the values k, c, d accordingly in the above formula we get,
Now, on further simplification we get,
Let us assume the area of the trapezium as A
Now, by substituting the respective values in the above area of the trapezium formula we get,
Let us now substitute the respective values.
Now, on subtracting the terms under the square root accordingly we get,
Now, on adding and multiplying the respective terms and further simplifying we get,
Now, on cancelling the common terms and rewriting the square root term we get,
Now, on further simplification we get,
Hence, the area of the given trapezium is 196 square metres.
Note: Instead of using the formula for area of trapezium when parallel and non-parallel sides are given we can use the normal formula that includes parallel sides and the height in which we need to find the height by using the non-parallel sides. Both the methods give the same result.
While calculating the area respective terms or side length should be substituted because neglecting any of the terms causes the square root to be unsolvable and then we cannot get the result. It is important to note that b should be greater than a because if not then the value of k will be negative which gives area as negative.
Complete step-by-step solution -
TRAPEZIUM:
If one pair of opposite sides of a quadrilateral are parallel, then it is called a trapezium.
Area of a trapezium when the length of the parallel sides and non-parallel sides are given is
Where,
a, b are the parallel sides
c, d are the non-parallel sides
Let us now draw the diagram of the trapezium.

Given, in the question that
Now, from the above formula k is given by
Now, by substituting the respective values of a and b we get,
Let us now find the value of s from the above formula
Now, by substituting the values k, c, d accordingly in the above formula we get,
Now, on further simplification we get,
Let us assume the area of the trapezium as A
Now, by substituting the respective values in the above area of the trapezium formula we get,
Let us now substitute the respective values.
Now, on subtracting the terms under the square root accordingly we get,
Now, on adding and multiplying the respective terms and further simplifying we get,
Now, on cancelling the common terms and rewriting the square root term we get,
Now, on further simplification we get,
Hence, the area of the given trapezium is 196 square metres.
Note: Instead of using the formula for area of trapezium when parallel and non-parallel sides are given we can use the normal formula that includes parallel sides and the height in which we need to find the height by using the non-parallel sides. Both the methods give the same result.
While calculating the area respective terms or side length should be substituted because neglecting any of the terms causes the square root to be unsolvable and then we cannot get the result. It is important to note that b should be greater than a because if not then the value of k will be negative which gives area as negative.
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Chandigarh is the capital of A Punjab B Haryana C Punjab class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE




