Question

A film of soap solution is trapped between a vertical frame and a light wire ab of length $0.1m$. If $g = 10m{s^{ - 2}}$, then the load $W$ that should be suspended wire to keep it in equilibrium is
A) $0.2g$
B) $0.3g$
C) $0.4g$
D) $0.5g$

Answer 1

Hint: Remember always that the weight of the load will always be equal to the surface tension. A soap bubble has two surfaces. So, the surface tension and the weight of the bubble are equal.

Formula used:
${\text{surface tension = }}\dfrac{{Force}}{{Length}}$
$ \Rightarrow F = S\left[ L \right]$
$ \Rightarrow F = S\left[ {{\text{Length of body which is in contact with liquid surface}}} \right]$
Where $F$ is the force, $S$ is the surface tension, $L$ is the length.

Complete step by step answer:
In gases, the intermolecular distance is relatively more. So the molecules are not influenced by neighboring molecules to hold them together. In liquids, molecules are relatively nearer when compared to gas molecules. So they are bound with intermolecular forces.
Surface tension is defined as the tangential force per unit length, acting at right angles to the liquid surface in equilibrium.
Let $F$ be the total force acting at one side of line. From the definition of surface tension,
${\text{surface tension = }}\dfrac{{Force}}{{Length}}$
$ \Rightarrow S = \dfrac{F}{l}$
Where $F$ is the force, $S$ is the surface tension, $l$ is the length.
Maximum surface tension force,
 $ \Rightarrow F = S\left[ L \right]$
$F = S\left[ {Length{\text{ }}of{\text{ }}body{\text{ }}which{\text{ }}is{\text{ }}in{\text{ }}contact{\text{ }}with{\text{ }}liquid{\text{ }}surface} \right]$
Given, Length of the wire \[L = 0.1m\].
Surface tension, $S = 25 \times {10^{ - 3}}N{m^{ - 1}}$

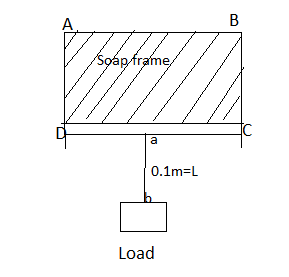
Consider an ABCD frame of soap solution. $ab$ is the length of the wire hanged by a load $W$.
When a wire A, B is pulled download through the weight of load $W$ then due to surface tension the force required to keep A, B in equilibrium is
 $ \Rightarrow F = S \times 2L$
We can calculate the total force by multiplying the surface tension with twice the length of the body that it is in contact with the liquid surface.
Since there are two surfaces of the soap solution.
That is, weight of the load = surface tension force
$W = F$
$ \Rightarrow mg = 2Sl$
$ \Rightarrow m = \dfrac{{2Sl}}{g}$
$ \Rightarrow \dfrac{{2 \times 25 \times {{10}^{ - 3}} \times 0.1}}{{10}}$
$ \Rightarrow m = 0.5 \times {10^{ - 3}}kg$
$\therefore 0.5g$

Therefore, correct option is (D).

Additional information:
There are two types of molecular forces of attraction among molecules. They are (i) forces of adhesion or adhesive forces and (ii) forces of cohesion or cohesive force.
Adhesion: the force of attraction among the molecules of different substances is called the force of adhesion.
Cohesion: The force of attraction among the molecules of the same substance is called the force of cohesion.

Note:
Applications of surface tension
(a) When a shaving brush is just dipped in water its hair spreads out. On taking out the brush from water the water film between the hair brings the hair closer, due to surface tension. Hence, the hairs of shaving brush or paintbrush when taken out of the water are pressed together.
(b) The end of the glass rod becomes round on heating.
(c) Hairs set well when oil is applied.
(d) Raindrops are spherical in shape. This is because a liquid drop tries to have a minimum surface area due to surface tension.