Question

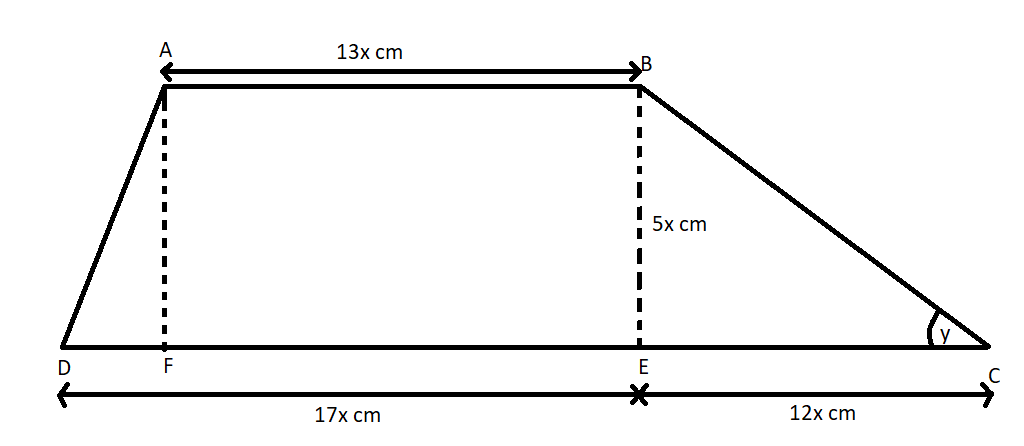
(A) Find the area of the trapezium in terms of x and simplify your answer?
(B) Angle \[{\rm{BCD = y}}\]. Calculate the value of y.

Answer 1

Hint:
Here, we have to use the basic concept of area to find out the area of the trapezium. Firstly we will divide the trapezium into simple shapes like divide it into two triangles and one rectangle. Then we have to find the area of those simple shapes in terms of x and addition of the area of the simple shapes will give us the area of the trapezium. In the second part we have to find out the angle y. So, by simply using the trigonometry formula we will get the value of the angle y.

Complete step by step solution:
ABCD is the given trapezium. So, we have to divide the given trapezium into the simple shapes i.e. two triangles ADF, BCE and one rectangle ABEF.
It is given that \[{\rm{AB = EF = 13x cm, AF = BE = 5x cm}},{\rm{ CE = 12x cm, DE = 17x cm}}\]
Now we have to find the area of these simple shapes i.e. triangle ADF, BCE and rectangle ABEF.
Therefore, area of triangle ADF\[ = \dfrac{1}{2} \times {\rm{Base}} \times {\rm{Height = }}\dfrac{1}{2} \times {\rm{DF}} \times {\rm{AF}}\]
It is given that \[{\rm{AF = 5x cm}}\] and \[{\rm{DF = DE}} - {\rm{FE = 17x}} - 13{\rm{x = 4x cm}}\]
Therefore, area of triangle ADF \[{\rm{ = }}\dfrac{1}{2} \times {\rm{DF}} \times {\rm{AF = }}\dfrac{1}{2}{\rm{(4x)(5x) = }}\dfrac{{20{{\rm{x}}^2}}}{2}{\rm{ = 10}}{{\rm{x}}^2}{\rm{ c}}{{\rm{m}}^2}\]
Now area of the triangle BCE \[ = \dfrac{1}{2} \times {\rm{Base}} \times {\rm{Height = }}\dfrac{1}{2} \times {\rm{CE}} \times {\rm{BE}}\]
Therefore, area of the triangle BCE \[{\rm{ = }}\dfrac{1}{2} \times {\rm{CE}} \times {\rm{BE = }}\dfrac{1}{2}{\rm{(12x)(5x) = }}\dfrac{{60{{\rm{x}}^2}}}{2}{\rm{ = 30}}{{\rm{x}}^2}{\rm{ c}}{{\rm{m}}^2}\]
Now we have to find out the area of the rectangle ABEF\[{\rm{ = Length}} \times {\rm{width = AB}} \times {\rm{BE}}\]
Therefore, area of the rectangle ABEF \[{\rm{ = AB}} \times {\rm{BE = (13x)}} \times {\rm{(5x) = 65}}{{\rm{x}}^2}{\rm{ c}}{{\rm{m}}^2}\]
Now as the area of the trapezium is the total sum of the area of the basic shapes i.e. two triangles and one rectangle.
\[{\text{Area of the trapezium ABCD}} = {\text{Area of triangle ADF}} + {\text{Area of the rectangle ABEF}} + {\text{Area of the triangle BCE}}\]
Therefore, area of the trapezium \[{\rm{ = 10}}{{\rm{x}}^2}{\rm{ + 65}}{{\rm{x}}^2} + {\rm{30}}{{\rm{x}}^2}{\rm{ = 105}}{{\rm{x}}^2}{\rm{ c}}{{\rm{m}}^2}\]
Hence \[{\rm{105}}{{\rm{x}}^2}{\rm{ c}}{{\rm{m}}^2}\]is the area of the given trapezium ABCD.

(B) In this we have to find out the angle y in the trapezium. So we have to use the trigonometry formula to find out the angle y.
So, in right triangle BCE right angle at E, we know that \[{\text{tan y = }}\dfrac{{{\text{side opposite to angle y}}}}{{{\text{side adjacent to angle y}}}}\]
Therefore, \[{\text{tan y = }}\dfrac{{{\rm{BE}}}}{{{\rm{CE}}}}{\rm{ = }}\dfrac{{5{\rm{x}}}}{{12{\rm{x}}}} = \dfrac{5}{{12}}\]
\[ \Rightarrow {\rm{y = ta}}{{\rm{n}}^{ - 1}}\left( {\dfrac{5}{{12}}} \right){\rm{ = 22}}{\rm{.6}}{{\rm{1}}^0}\]

Hence, \[{\rm{22}}{\rm{.6}}{{\rm{1}}^0}\] is the value of angle y.

Note:
Right Triangle is a triangle where one of its interior angles is a right angle (90 degrees). The relation between the sides and angles of a right triangle is the basis for trigonometry. The side opposite the right angle is called the hypotenuse. The sides adjacent to the right angle are called legs.
Pythagoras theorem stated that in a right angled triangle the square of the long side is equal to the sum of the squares of the other two sides.
We have to remember all the trigonometry formulas
\[{\text{sin A = }}\dfrac{{{\text{side opposite to angle A}}}}{{{\text{hypotenuse}}}}\], \[{\text{cos A = }}\dfrac{{{\text{side adjacent to angle A}}}}{{{\text{hypotenuse}}}}\], \[{\text{tan A = }}\dfrac{{{\text{side opposite to angle A}}}}{{{\text{side adjacent to angle A}}}}\], \[{\text{cot A = }}\dfrac{1}{{{\text{tan A}}}}\], \[{\text{sec A = }}\dfrac{1}{{{\text{cos A}}}}\], \[{\text{cosec A = }}\dfrac{1}{{{\text{sin A}}}}\]