Question

A force $5\text{ N}$ acts on a particle along a direction making an angle of ${60}^{\circ }$ with vertical. Its vertical component be
A. $\text{10 N}$
B. $\text{3 N}$
C. $\text{4 N}$
D. $2.5\text{ N}$

Answer 1

Hint:We are given a particle making a certain angle with the vertical and a force of certain magnitude is acting on it along the direction of the vertical and we need to find the vertical component of the force for which we need to draw a rough diagram and resolve the force into its horizontal and vertical component.

Complete step by step answer:
Let us make a rough diagram to get a better understanding of the situation

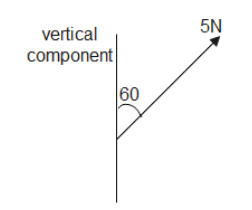
We can break the force acting on the particle into its vertical and horizontal component.
We know that the vertical component is given by $F\cos \theta$ where $\theta$ is the angle between the force acting on the particle and the vertical which is given.
$F_{vertical}=F\cos \theta$
Therefore by substituting the values of force and angle we get
$F_{vertical}=5\cos {60}^{\circ }$
$\therefore F_{vertical}=2.5\text{ N}$

Therefore option D is the correct answer.

Additional information:: In mechanics, force is defined as any action that tends to maintain or alter the motion of a body or to distort it. The concept of force is defined by Newton’s law of motion. Force is a vector quantity and the representation of force by vectors implies that they are concentrated either at a single point or along a single line.

Note: The force is a vector quantity meaning it has both magnitude and direction. And like every vector it can be resolved into two components. The vertical component is along the y-axis if we consider the force acting on a cartesian plane and the horizontal component is along the x-axis. These components represent the force acting in the vertical and the horizontal direction respectively.