Question

A fruit grower can use two types of fertilizer in his garden, brand P and brand Q. The amounts (in kg) of nitrogen, phosphoric acid, potash, and chlorine in a bag of each brand are given in the table. Tests indicate that the garden needs at least 240 kg of phosphoric acid, at least 270 kg of potash, and at most 310 kg of chlorine.
If the grower wants to minimize the amount of nitrogen added to the garden, how many bags of each brand should be used? What is the minimum amount of nitrogen added in the garden?

Kg per bag	Brand P	Brand Q
Nitrogen	3	3.5
Phosphoric acid	1	2
Potash	3	1.5
Chlorine	1.5	2

Answer 1

Hint: First of all, we will assume some variables for the number of bags of brand P and the number of bags of brand Q. Then, according to the given information, we will form linear equations and plot them in the graph and find a region of possible values of those variables, in which all the required conditions are satisfied. Since we are asked to find the number of bags so that the nitrogen in his garden is minimum, if we have multiple points that satisfy the conditions, we will select the combination with minimum nitrogen.

Complete step by step answer:
Let us assume that the number of bags of brand P required for the garden is x and the number of bags of brand Q required is y.
It is given that the garden needs at least 240 kg of phosphoric acid. From the table we can see that each bag of brand P has 1 kg of phosphoric acid and each bag of Q has 2 kg of phosphoric acid.
$\Rightarrow x+2y\ge 240......\left( 1 \right)$
It is also given that the garden needs at least 270 kg of potash. From the table we can see that each bag of brand P has 3 kg of potash and each bag of Q has 1.5 kg of potash.
$\begin{align}
  & \Rightarrow 3x+1.5y\ge 270 \\
 & \Rightarrow 2x+y\ge 180......\left( 2 \right) \\
\end{align}$
And we also know that the garden needs at most 310 kg of chlorine. From the table we can see that each bag of brand P has 1.5 kg of chlorine and each bag of Q has 2 kg of chlorine.
$\begin{align}
  & \Rightarrow 1.5x+2y\le 310 \\
 & \Rightarrow 3x+4y\le 620......\left( 3 \right) \\
\end{align}$
The nitrogen content cannot be negative in the garden. From the table we can see that each bag of brand P has 3 kg of nitrogen and each bag of Q has 3.5 kg of nitrogen.
$\begin{align}
  & \Rightarrow 3x+3.5y\ge 0 \\
 & \Rightarrow 6x+7y\ge 0......\left( 4 \right) \\
\end{align}$
We will graph all the 4 lines on a graph.

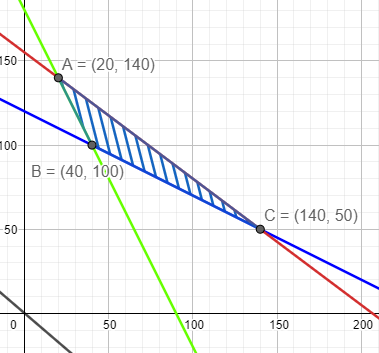
Here, the x – coordinate denotes the number of bags of brand P and y – coordinate shows the number of bags of brand Q.
The hatched region shows the region of points which satisfy all the conditions.
We can safely say that the nitrogen will be minimum at one of the corner points.
The corner points are (20, 140), (40, 100) and (140, 50).
The amount of nitrogen will be given as Z = 3x + 3.5y.
The amount of nitrogen if x = 20 and y = 140 is Z = 3(20) + 3.5(140) = 550 kg.
The amount of nitrogen if x = 40 and y = 100 is Z = 3(40) + 3.5(100) = 470 kg.
The amount of nitrogen if x = 140 and y = 50 is Z = 3(140) + 3.5(50) = 595 kg.
Hence, to minimize the amount of nitrogen, the number of bags of brand P should be 40, and number of bags of brand Q should be 100.
The amount of nitrogen with this combination will be 470 kg.
Note:
Students can solve this question using the analytical method also by solving the given 4 linear equations. They can opt for any of the 3 available methods of solving linear equations in 2 variables. Solving analytically will only give the corner points and not the feasible region.