
A frustum of a pyramid has an upper base 100m by 10m and a lower base of 80m by 8m, if the altitude of the frustum is 5m, find the volume of the frustum (in cu. m.)
A. 4567.67
B. 3873.33
C. 4066.67
D. 2345.98
Answer
503.4k+ views
1 likes
Hint: In this particular problem apply the direct formula for the volume of frustum that is
Complete step by step answer:
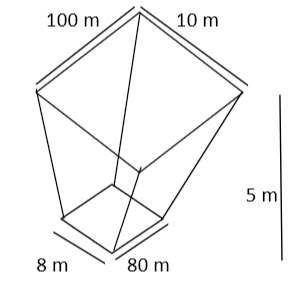
As we know that to find the volume of the frustum first, we had to find the area of its upper and lower base.
Now as we can see from the above figure that the lower and upper base of the frustum is in rectangle shape.
And the area of the rectangle is calculated as
So, let the area of the upper base of the rectangle be
So,
And let the area of the lower base of the rectangle be
So,
And it is given that the height (altitude) of the frustum is 5m.
So, now let us the put the values in the formula of volume of frustum that is
So, the volume of the frustum will be =
Hence, the correct option will be C.
Note: Whenever we face such types of problems then first, we have to find the area of the rectangle using the formula
Complete step by step answer:

As we know that to find the volume of the frustum first, we had to find the area of its upper and lower base.
Now as we can see from the above figure that the lower and upper base of the frustum is in rectangle shape.
And the area of the rectangle is calculated as
So, let the area of the upper base of the rectangle be
So,
And let the area of the lower base of the rectangle be
So,
And it is given that the height (altitude) of the frustum is 5m.
So, now let us the put the values in the formula of volume of frustum that is
So, the volume of the frustum will be =
Hence, the correct option will be C.
Note: Whenever we face such types of problems then first, we have to find the area of the rectangle using the formula
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




