
A gas is compressed isothermally to half of its initial volume. The same gas is compressed separately through an adiabatic process until its volume is again reduced to half. Then
a) Compressing the gas isothermally will require more work to be done.
b) Compressing the gas adiabatically will require more work to be done.
c) Compressing the gas adiabatically or isothermally will require the same amount of work.
d) Which of the cases(whether compression through isothermal or through adiabatic process)requires more work will depend upon the atomicity of the gas?
Answer
481.5k+ views
Hint: In the question it is said that the same gas is compressed isothermally as well as adiabatically. The compression is done such that both the gases are compressed half of their initial volumes. Hence we will under the PV curve which of the following curves will have a greater area which will tell us the work done will be more than with respect to others.
Formula used:
Complete step-by-step answer:
Basically in the above question our aim is to determine the area under the PV curve for adiabatic and isothermal curves. Let us say the pressure is P and volume is V at a particular point on the in both the adiabatic and isothermal process.
In case of an isothermal process product of pressure times the volume is basically a constant K. Mathematically this can be represented as,
But in the adiabatic process we represent the relation between pressure and volume as,
Now let us write the differential forms of the above equation in order to obtain their slopes. The slopes of the either curve is nothing but a ratio of small change in pressure(dP) with respect to small change in volume (dV). The differential form of equation of isothermal process we get,
Similarly, The differential form of equation of adiabatic process we get,
Since
So, the correct answer is “Option a”.
Note: Figure below depicts the above scenario.
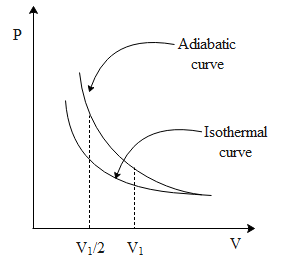
Isothermal process is a thermodynamic process carried out at constant temperature. Similarly, in adiabatic process there is neither no transfer of heat from the system to the surrounding nor vice-versa. In the above figure between any two points of the same volume we can see that work done for adiabatic is greater than that of isothermal.
Formula used:
Complete step-by-step answer:
Basically in the above question our aim is to determine the area under the PV curve for adiabatic and isothermal curves. Let us say the pressure is P and volume is V at a particular point on the in both the adiabatic and isothermal process.
In case of an isothermal process product of pressure times the volume is basically a constant K. Mathematically this can be represented as,
But in the adiabatic process we represent the relation between pressure and volume as,
Now let us write the differential forms of the above equation in order to obtain their slopes. The slopes of the either curve is nothing but a ratio of small change in pressure(dP) with respect to small change in volume (dV). The differential form of equation of isothermal process we get,
Similarly, The differential form of equation of adiabatic process we get,
Since
So, the correct answer is “Option a”.
Note: Figure below depicts the above scenario.

Isothermal process is a thermodynamic process carried out at constant temperature. Similarly, in adiabatic process there is neither no transfer of heat from the system to the surrounding nor vice-versa. In the above figure between any two points of the same volume we can see that work done for adiabatic is greater than that of isothermal.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




