Question

A girl wishes to prepare birthday caps in the form of right circular cones for her birthday party, using a sheet of paper whose area is 5720 \[c{m^2}\], how many caps can be made with radius 5 cm and height 12 cm.

Answer 1

Hint: In this particular problem we have to find the curved surface area of one cone using formula \[\pi rl\], where r is the base radius and l is the slant height. And then divide this area with the total area given to find the required answer.

Complete step by step answer:

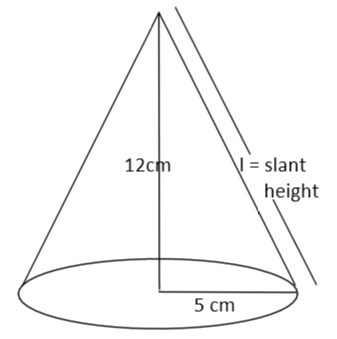
As we know, the base radius of the cone is 5 cm.
And the height of the cone is 12 cm.
Now to find the area of the cone we had to find the slant height of the cone.
Now as we know that the formula for slant height of the cone is \[l = \sqrt {{r^2} + {h^2}} \], where r and h are the base radius and height of the cone.
So, let us find the slant height of the cone (birthday cap).
Slant height = \[\sqrt {{5^2} + {{12}^2}} = \sqrt {25 + 144} = \sqrt {169} = 13\]cm.
So, now we can find the curved surface area of one birthday cap.
Curved surface area of one cap = \[\pi rl = \pi \times \left( 5 \right) \times \left( {13} \right) = 65\pi c{m^2}\].
Now as we know that if the area of one cap is \[65\pi c{m^2}\] then the number of caps that can be made in the given sheet of paper = \[\dfrac{{{\text{Area of sheet of paper}}}}{{{\text{Area of one cap}}}} = \dfrac{{5720}}{{65\pi }} = \dfrac{{5720}}{{65 \times \dfrac{{22}}{7}}} = \dfrac{{5720 \times 7}}{{65 \times 22}} = \dfrac{{40040}}{{1430}} = 28\]
Hence, 28 birthday caps can be made from the sheet of the paper.
Note:
Whenever we face such types of problems then we should remember that the birthday cap is open from the bottom. So, while making a birthday cap, no sheet of paper is required for covering the bottom so we have to find a curved surface area instead of a total surface area of one cone. And then we had to divide that with the area of the sheet of paper given to find the total number of caps that can be made. This will be the easiest and efficient way to find the solution of the problem.